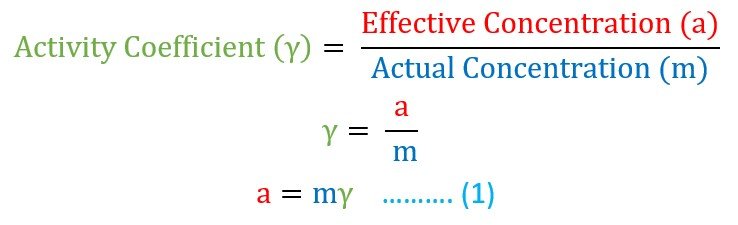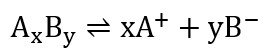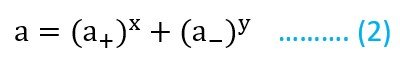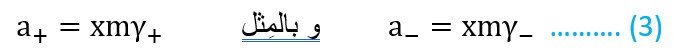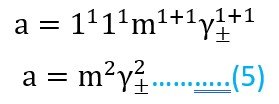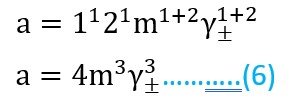الفعالية و معامل الفعالية Activity and Activity Coefficient

الفعالية و معامل الفعالية Activity and Activity Coefficient

في العام 1908 قام العالم لويس بتقديم مصطلح الفعالية activity و معامل الفعالية activity coefficient من أجل شرح و توضيح سبب انحراف المحلول الإلكتروليتي أو الغاز عن السلوك المثالي .

فعندما يكون المحلول مخفف جدا فإن ذلك يعني أنه قد تم تفككه بالكامل إلى أيونات و بالتالي يصبح مثاليا للتوصيل الكهربائي، و يطلق على هذا المحلول اسم المحلول المثالي ، و لمثل هذا المحلول المثالي فإن التركيز الفعال (الملاحظ) يكون مساويا للتركيز الفعلي (النظري).

و لكن في حال الإلكتروليت (محلول يوصل التيار الكهربائي عند تذويبه في الماء) فإنه لا يتفكك بالكامل و في هذه الحالة فإن التركيز الفعال a (الملاحظ)  يكون دائما أقل منه التركيز الفعلي m (النظري). لذلك قام لويس بتقديم أو طرح مفهوم معامل الفعالية و الذي يرمز له بالرمز جاما (γ) لشرح الانحراف عن السلوك المثالي.

لنفترض الآن لدينا إلكتروليت صيغته الكيميائية A_xB_y ، و هذا الإلكتروليت تفكك جزئيا حسب التفاعل الآتي :

هذا يعني أن مولا واحدا من A_xB_y انتج في المحلول x مولات من الكاتيون (⁺A) و y مولات من الأنيون (^–B) . لذلك يمكننا القول أنه يمكن تعريف فعالية الإلكتروليت أعلاه بأنها نتاج لفعاليات كل من الكاتيونات (₊a) و الأنيونات (_–a) ، و عليه يمكننا القول أن الفعاليـة العامة للمحلول تساوي :

بالرجوع إلى العلاقة رقم (1) يمكننا القول أن فاعلية الكاتيون (₊a) تساوي

حيث ₊m تركيز الكاتيون و ₊γ معامل الفعالية للكاتيون. و لطالما مولا واحدا من الإلكتروليت ينتج x مولات من الكاتيون، فإن تركيز الكاتيون سوف يساوي x مرات تركيز الإلكترويت ( m₊ = xm ) . إذن ، يمكننا القول بأن :

و بتعويض القيم السابقة في المعادلة رقم (2) ، نحصل على :

حيث _±γ متوسط معامل الفعالية . لذلك يمكننا القول بأن :

الحالة الأولى : فلنفترض أن لدينا إلكتروليت أحادي-أحادي التكافؤ مثل NaCl و KCl … إلخ ، فإنه في حالة NaCl مثلا فإن قيمة x تساوي 1 ، و قيمة y تساوي 1 ، لذلك يمكننا كتابة المعادلة رقم 4 على النحو الآتي :

الحالة الثانية: فلنفترض أن لدينا إلكتروليت أحادي-ثنائي التكافؤ مثل ZnCl₂ و Na₂CO₃… إلخ ، فإنه في حالة ZnCl₂ مثلا فإن قيمة x تساوي 1 ، و قيمة y تساوي 2 ، لذلك يمكننا كتابة المعادلة رقم 4 على النحو الآتي :

الحالة الثالثة: فلنفترض أن لدينا إلكتروليت أحادي-ثلاثي التكافؤ مثل AlCl₃ و Na₂CO₃… إلخ ، فإنه في حالة ZnCl₂ مثلا فإن قيمة x تساوي 1 ، و قيمة y تساوي 3 ، لذلك يمكننا كتابة المعادلة رقم 4 على النحو الآتي :

 

المصادر:

• الموسوعة العلمية الكيميائية للأستاذ أكرم العلي
• https://www.youtube.com/watch?v=3edwwLc7KO8

بوسترات (لوحات) كيميائية بدقة عالية (أكثر من 25 لوحة) من تصميم الأستاذ أكرم أمير العلي

 

تطبيقات كيميائية من تصميم الأستاذ أكرم امير العلي متوفر للجوالات التي تعمل بنظام أندرويد android على سوق جوجل بلاي google play

1 – تطبيق ملصقات الجدول الدوري باللغة العربية : بطاقات تحتوي على معلومات شاملة و مختصرة في نفس الوقت كل عنصر على حدة (اللغة العربية).

https://play.google.com/store/apps/details?id=com.akramir2