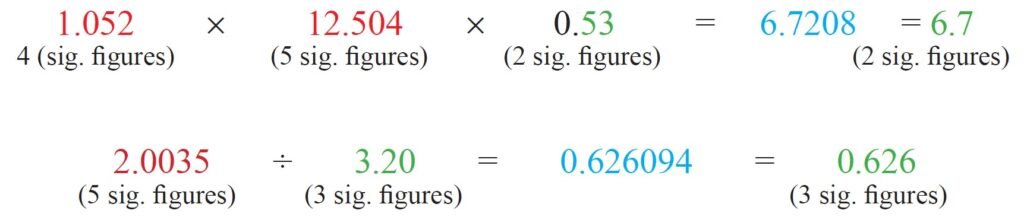الأرقام المعنوية Significant Figures

الأرقام المعنوية Significant Figures

عادة ما يدون العلماء الكميات المقاسة بطريقة قياسية متفق عليها، و عادة ما يعكس عدد الأرقام المكتوبة في التقرير مدى الدقة في القياس: فكلما كان هناك مزيدا من الأرقام كانت الدقة أعلى، و على النقيض تماما كلما كانت الأرقام أقل كانت الدقة أقل. و عادة ما تتم كتابة الأرقام بحيث يكون الرقم الأخير هو الرقم المشكوك فيه .
فمهما كانت الاجهزة التي تستخدمها للقياس دقيقة جدا إلا أنه من المستحيل الحصول على قراءة دقيقة للكمية قيد الدراسة. فمثلا لو أردنا أن نقيس كتلة عملة معدنية على ميزان حساس جدا و قادر على القياس إلى أقرب 0.0001 جم.فإنه يمكننا أن ندون الكتلة على أنها تساوي 2.2405 مع هامش خطأ مقدارة 0.0001 جم. ، و عليه يمكننا أن نكتب كما يلي :0.0001±2.2405 و يقصد بالرمز± (تقرأ «زائد أو ناقص») عن مقدار الشك في القياس، أي أن الرقم الأخير غير مؤكد أو مشكوك في أمره.
و تسمى جميع أرقام الكمية المقاسة ، بما في ذلك الرقم المشكوك في أمره ، بالأرقام المعنوية. فللكتلة المقاسة و المسجلة على أنها 2.2 غرام فإن لها رقمان معنويان، في حين أن الكتلة المسجلة على أنها 2.2405 جم لها خمسة أرقام معنوية . و عليه يمكننا القول بأنه كلما زاد عدد الأرقام المعنوية، زادت الدقة الضمنية للقياس.
و لكن في الكثير من الأبحاث العلمية ، لا يتم كتابة الرمز ± و عادة ما يكون مفهوم ضمنيا أن هناك قدر من الشك في الرقم الأخير لأي كمية مقاسة.
و الآن لنفترض أننا نريد قياس حجم كمية معينة من السائل باستخدام المخبار المدرج حيث دقة المخبار ±1 مل في القياس.فإذا وجد أن الحجم هو 6 مل ، فإن الحجم الفعلي قد يكون في حدود 5 مل إلى 7 مل.و عادة ما نكتب حجم السائل بالصيغة التالية (1±6) مل. في هذه الحالة ، لا يوجد سوى رقم واحد معنوي و هو (الرقم 6) و الذي هو بحد ذاته مشكوك فيه إما زائد أو ناقص 1 مل. و لمزيد من الدقة ، قد نستخدم مخبار مدرج يحتوي على أقسام أدق ، بحيث يصبح حجم القياس الذي نقيسه مشكوك فيه الآن بنسبة ±0.1 مل فقط. فإذا كان حجم السائل هو 6.0 مل ، فإننا نعبر عن الكمية على أنها (0.1±6.0) مل، و عليه فإن القيمة الفعلية تتراوح بين 5.9 مل و 6.1 مل، و لاحظ هنا أنه أصبح لدينا رقمان معنويان و بالتالي دقة القياس أصبحت أعلى.
يمكننا تحسين جهاز القياس والحصول على أرقام معنوية أكثر ، ولكن في كل حالة، يكون الرقم الأخير مشكوك فيه دائمًا ؛ و يعتمد مقدار الشك هذا على جهاز القياس المحدد الذي نستخدمه.كما تكمن أهمية الارقام المعنوية هو التأكد من أن الأجابة النهائية التي سوف تحصل عليها ليست أكثر دقة من القراءات أو الأعداد التي بدأت بها.

 

قواعد تحديد الأرقام المعنوية

يجب أن نكون دائمًا حذرين دائما في العمل المخبري العلمي عند تدوين و كتابة الأرقام المعنوية . و بشكل عام ، من السهل إلى حد ما تحديد عدد الأرقام المعنوية التي يملكها الرقم باتباع القواعد التالية:

1. أي رقم ليس صفراً يعتبر رقم معنوي. وبالتالي ، فإن الرقم 635 سم فيه ثلاثة أرقام معنوية، و الرقم 3.485 كيلوجرام فيه أربعة أرقام معنوية ، وهكذا.
2. الأصفار بين الأرقام غير الصفرية تعتبر أرقاما معنوية . وهكذا ، فمثلا الرقم 408 متر فيه ثلاثة أرقام معنوية و الرقم 40.501 كيلوجرام يحتوي على خمسة أرقام معنوية.
3. الأصفار الموجودة على يسار أول رقم غير صفري (الأصفار البادئة) ليست أرقاما معنوية، فالغرض منها هو الإشارة إلى موضع العلامة العشرية. على سبيل المثال، يحتوى الرقم 0.06 لتر على رقم معنوي واحد ، و الرقم 0.0000742 جرام يحتوي على ثلاثة أرقام معنوية ، وهكذا.
4. إذا كان الرقم على يسار العلامة العشرية أكبر من 1 ، فسيتم اعتبار جميع الأصفار المكتوبة على يمين العلامة العشرية أرقاما معنوية معنوية. لذلك ، الرقم 2.0 مليجرام له رقمان معنويان ، و الرقم 40.062 مليلتر له خمسة أرقام معنوية، و الرقم 3.040 ديسيمتر له أربعة أرقام مهمة. أما إذا كان الرقم قبل العلامة العشرية أقل من 1 ، فستكون الأصفار الموجودة في نهاية الرقم والأصفار الموجودة بين أرقام غير صفرية فقط أرقاما معنوية. هذا يعني أن 0.090 كيلوجرام لها رقمان مهمان ، 0.3005 لتر لها أربع أرقاما معنوية ، و 0.00420 دقيقة لها ثلاثة أرقام معنوية، وهكذا.
5. الأصفار اللاحقة و التي تأتي بعد الفاصلة العشرية دائما تكون أرقاما معنوية. مثال : 45.000 جرام (خمسة أرقاما معنوية).
6. الأصفار اللاحقة و التي تأتي قبل العلامة العشرية و بعد الرقم اللاصفري دائما أرقاما معنوية. فالرقم 2500.55 له ستة أرقاما معنوية.
7. الأصفار التي توجد في نهاية الرقم و قبل العلامة العشرية الضمنية (علامة عشرية غير مكتوبة) تعتبرمبهمة ويجب تجنبها باستخدام الترميز العلمي.فمثلا قد يكون للرقم 400 سنتيمتر رقم واحدة معنوي (الرقم 4) ، أو رقمان معنويان (40) ، أو ثلاثة أرقام معنوية (400). لذلك لا يمكننا معرفة ما هو الصحيح دون مزيد من المعلومات. و لكن باستخدام التدوين العلمي يمكننا أن نتجنب هذا الغموض. ففي هذه الحالة بالذات ، يمكننا التعبير عن الرقم 400 على شكل 10² × 4 و هنا سـوف يكون لدينا رقم معنوي واحد أو 10² × 4.0 يكون لدينا رقمين معنويين ، أو 10² × 4.00 ثلاثة أرقام معنوية. و خلاصة ما سبق هو في حالة الأرقام المبهمة إذا وجدت الفاصلة العشرية في نهاية الأصفار اللاحقة فإن تلك الأصفار تحسب أرقاما معنوية. فمثلا للرقم 70000 هناك رقما معنويا واحدا و هو 7 ، بينما للرقم .70000 (لاحظ الفاصلة العشرية نهاية الأصفار اللاحقة) فإنه يكون لدينا خمسة أرقاما معنوية.

و كذلك الحال بالنسبة للرقم 1030 فإنه لديه ثلاثة أرقاما معنوي (الصفر الأخير لا يحسب لانه لاتوجد علامة عشرية بعده) بينما للرقم 1030.0 هناك خمسة أرقاما معنوية (تم احتساب الصفر الاخير كرقم معنوي بسبب وجود العلامة العشرية) .

حسابات الأرقام المعنوية

عندما نستخدم الكميات المقاسة في العمليات الحسابية ، يجب أن تعكس نتائج الحساب دقة الكميات المقاسة. و هذا يعني أنه يجب أن ألا نفقد أو نكتسب الدقة أثناء الحسابات الرياضية. اتبع هذه القواعد عند التعامل مع الأرقام المعنوية أثناء العمليات الحسابية.

1. في عمليات الضرب أو القسمة ، فإن الناتج النهائي يجب أن يحوي على أرقاما معنوية مساويا لعدد الأرقام المعنوية في العدد الذي لديه أقل عدد من الأرقام المعنوية.

2. في عمليات الجمع أو الطرح ، يجب أن يحوي الناتج النهائي على عدد خانات عشرية مساويا لعدد الخانات العشرية في الرقم الذي لديه أقل عدد من الخانات العشرية.

عند الجمع أو الطرح ، من المفيد رسم خط بجانب الرقم الذي لديه أقل عدد من الخانات العشرية. و هذا الخط يحدد عدد الخانات العشرية في الإجابة.

ولاحظ مما سبق أنه في حالتي الضرب و القسمة تم الاخذ بعيسن الاعتبار الأرقام المعنوية و في حالتي الجمع و الطرح تم الاخذ بعن الاعتبار موقع العلامة العشرية.
في معظم العمليات الحسابية ، ستحتاج إلى تقريب الأرقام للحصول على العدد الصحيح من الأرقام المعنوية. لذلك يجب تطبيق القواعد التالية عند التقريب.

1. في الحسابات متعدد الخطوات، انقل الارقام الزائدة من خطوة لأخرى و من ثم قم بعملية التقريب في الناتج النهائي.
2. إذا تطلب الامر إزالة الرقم:

• أ – إذا كان أقل الرقم المطلوب حذفه أقل من 5 ، فإن الرقم الذي قبله يبقي كما هو. فمثلا يمكن تقريب الر قم 1.33 إلى 1.3 .
• ب – إذا كان الرقمك المطلوب حذفه يساوي أو أكبر من 5 ، فإن الرقم الذي قبله يزداد واحد. فمثلا الرقم 1.36 يقرب إلى 1.4 .

 

بوسترات (لوحات) كيميائية بدقة عالية (أكثر من 25 لوحة) من تصميم الأستاذ أكرم أمير العلي

 

تطبيقات كيميائية من تصميم الأستاذ أكرم امير العلي متوفر للجوالات التي تعمل بنظام أندرويد android على سوق جوجل بلاي google play

1 – تطبيق ملصقات الجدول الدوري باللغة العربية : بطاقات تحتوي على معلومات شاملة و مختصرة في نفس الوقت كل عنصر على حدة (اللغة العربية).

https://play.google.com/store/apps/details?id=com.akramir2