إتزان الحمض – القاعدة أحادي البروتون Monoprotic Acid- Base Equilibria

إتزان الحمض  – القاعدة أحادي البروتون

Monoprotic Acid- Base Equilibria

( Sections 8.1 – 8.5, Quantitative Chemical Analysis by Daniel C. Harris, 8th Edition )

( التحليل الكيميائي النوعي – دانيال هاريس )

8 – 1  الحموض و القواعد القوية

8 – 1 Strong Acids and Bases

Acids and Bases are essential to virtually every application of chemistry.

الحموض والقواعد ضرورية لكل تطبيقات الكيمياء تقريبًا.

Analytical procedures such as chromatography and electrophoresis.

تستخدم الحموض و القواعد في الإجراءات التحليلية مثل الكروماتوغرافيا والرحلان الكهربي

Protein purification, chemical reactions, environmental issues

كما تستخدم الحموض و القواعد في تنقية البروتين و التفاعلات الكيميائية و القضايا البيئية.

Strong Acids and Bases are completely dissociates.

تتفكك الحموض و القواعد بالكامل في محاليلها.

When strong acid react with strong base [H₃O⁺] or [OH^–] have equals concentration.

عندما يتفاعل حمض قوي و قاعدة قوية فإن تراكيز [^–OH] و [⁺H₃O] تكون متساوية.

To calculate pH of an acid we use the following equation.

لحساب قيمة الرقم الهيدروجيني للحمض فإننا نستخدم العلاقة الآتية:

pH = -log[H⁺]           ……….. (1)

To calculate pH using activity coefficients of an acid we use the following equation.

لحساب قيمة الرقم الهيدروجيني باستخدام معاملت الفعالية للحمض فإننا نستخدم العلاقة الآتية:

pH = -log[H⁺]γ_H⁺

To calculate pH of an base we use the following equation.

لحساب قيمة الرقم الهيدروجيني لقاعدة فإننا نستخدم العلاقة الآتية:

K_w = [H⁺][OH^–]

[H⁺] = ^K_w/_[OH^–]           ……….. (2)

pH = pOH = -logK_w = 14.00            ……….. (3)

Then we use equation 1 to calculate the pH

و من ثم نستخدم العلاقة رقم 1  لحساب قيمة الرقم الهيدروجيني pH

Example1 : What is the pH of a 0.1 M solution of HCl.

مثال1 : ما هي قيمة الرقم الهيدروجيني لمحلول حمض الهيدروكلوريك تركيزه 0.1 مول/لتر.

Solution: 

[H⁺] = [HCl] = 0.1 M

pH = -log[H⁺]

pH =-log(0.1M) = 1.00

Example2 : Calculate the pH of 0.10 M HBr, using activity coefficients.

مثال1 : احسب قيمة الرقم الهيدروجيني لمحلول حمض الهيدروبروميك تركيزه 0.10 مول/لتر باستخدام معاملات الفعالية.

Solution: 

[H⁺] = [HBr] = 0.1 M

Activity coefficient of H⁺ is 0.83

pH = -log[H⁺]γ_H⁺

pH =-log(0.10)(0.83) = 1.08

Example3 : Calculate the pH of 0.10 M KOH.

مثال1 : احسب قيمة الرقم الهيدروجيني لمحلول هيدروكسيد البوتاسيوم تركيزه 0.10 مول/لتر .

Solution: 

[OH^–] = [KOH] = 0.1 M

[H⁺] = ^K_w/_[OH^–] 

[H⁺] = ^1.0×10–14/0.10 

[H⁺] = 1.0×10^–13 M 

pH = -log[H⁺]

pH =-log(1.0×10^–13) = 13.00

*********The Dilemma مسألة إشكالية**********

When we calculate the pH of 0.1 × 10^–8 M KOH the result is 6 which is impossible (How can the base KOH produce an acidic solution). Clearly, there is something wrong with the calculation. In particular, we have not considered the contribution of OH^– from the ionization of water. In pure water, [OH^–] = 1.0 × 10^–7 M, which is greater than the amount of KOH added to the solution. To handle this problem, we resort to the systematic treatment of equilibrium.

عندما نحسب الرقم الهيدروجيني pH لمحلول هيدروكسيد البوتاسيوم KOH تركيزه ^8–10 × 0.1 ، تكون النتيجة 6 !! فكيف يمكن للقاعدة القوية KOH إنتاج محلول حمضي؟ فهذا امر مستحيل طبعا. من الواضح أن هناك خطأ ما في الحساب. على وجه الخصوص ، لم نأخذ في الاعتبار مساهمة ^–OH في المحلول الناتج عن تأين الماء. في الماء النقي ، [^–OH] = 1.0 × 10^–7 مول/لتر، وهي أكبر من كمية KOH المضافة إلى المحلول. و للتعامل مع هذه المشكلة ، نلجأ إلى المعالجة المنهجية للإتزان.

Step 1 Pertinent reactions. The only one  is:

الخطوة 1 التفاعلات ذات الصلة. هناك تفاعل واحد هو :

لاحظ هنا ان معادلة تفكك KOH ليست ذات صلة لان KOH تفكك بالكامل

Step 2 The charge balance. The species in solution are K⁺, OH^–, and H⁺. So,

الخطوة 2 توازن الشحنة. الجسيمات الموجودة في المحلول هي ⁺K و ^–OH و ⁺H ، لذلك :

[K⁺] = [H⁺] + [OH^–]          ……….. (4)

Step 3 Mass balance . All K⁺ comes from the KOH, so :

الخطوة 3 توازن الكتلة. جميع أيونات البوتاسيوم  ⁺K مصدرها KOH ، لذلك فإن :

[K⁺] = 1.0 × 10^–8 M

Step 4 Equilibrium constant.

الخطوة 4 ثابت الاتزان .

K_w = [H⁺][OH^–] = 1.0 × 10^–14 

Step 5 Count the equations and unknowns. There are three equations and three unknowns ([H⁺], [OH^–], [K⁺]), so we have enough information to solve the problem.

الخطوة 5 حساب و عد المعادلات و المجاهيل. هناك ثلاثة معادلات و ثلاثة مجاهيل ([⁺H], [^–OH], [⁺K]) ، لذلك لدينا معلومات كافية لحل المسألة.

Step 6 Solve for all unknowns. We seek the pH, so let’s set [H⁺] = x. Writing [K⁺] = 1.0 × 10^–8 M in Equation 4, we get

الخطوة 6 حل كل المجاهيل. ما نريده هو قيم الرقم الهيدروجيني pH ، لذلك لنفترض بأن [⁺H] تساوي x . و بالتعويض بقيمة  و التي تساوي ^8–10 × 1.0 مول/لتر في المعادلة رقم 4 نحصل على:

[OH^–] = [K⁺]+[H⁺] = 1.0 × 10^–8 + x

********************

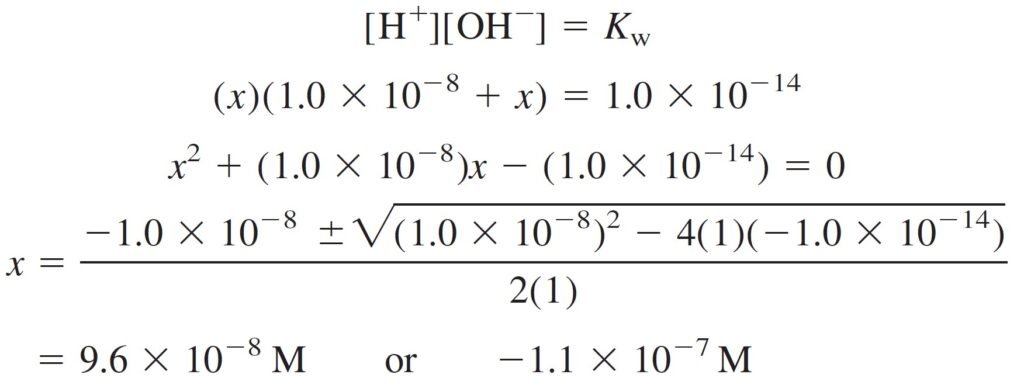
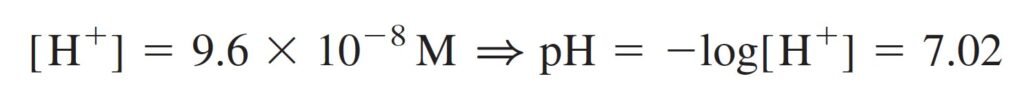
By studying the following figure which shows the pH calculated for different concentrations of strong base or strong acid in water, we find that there are three regions:

بدراسة الشكل التالي و الذي يوضح قيمة الرقم الهيدروجيني المحسوبة لتركيزات مختلفة من القاعدة القوية أو الحمض القوي في الماء ، نجد أن هناك ثلاث مناطق:

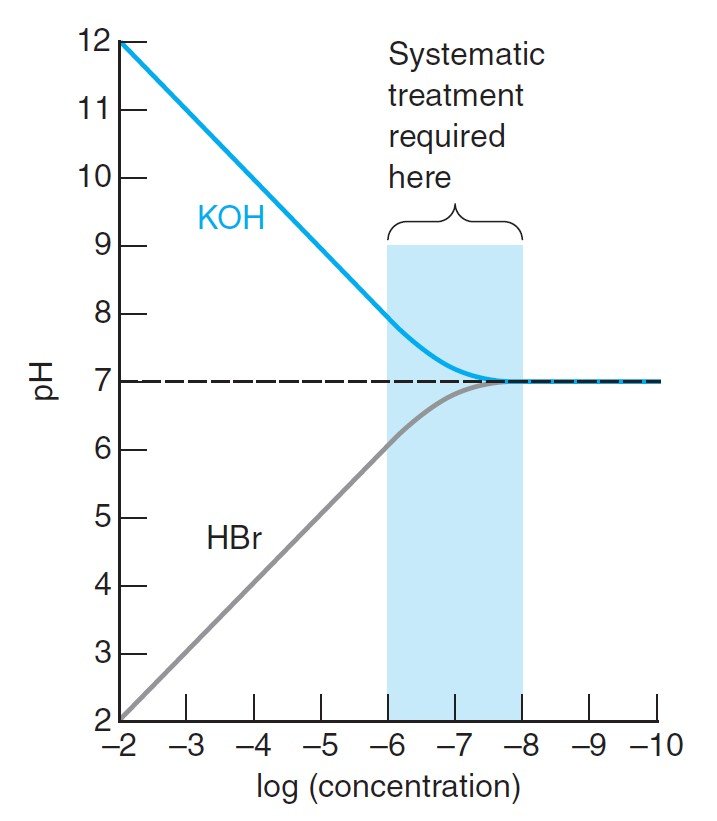
1. When the concentration is “high” (≥10^–6 M), pH is calculated by just considering the added H⁺ or OH^–.
2. When the concentration is “low” (≤10^–8 M), the pH is 7.00. We have not added enough acid or base to change the pH of the water itself.
3. At intermediate concentrations of 10^–6 to 10^–8 M, the effects of water ionization and the added acid or base are comparable. Only in this region is a systematic equilibrium calculation necessary.

 

1. عندما يكون التركيز “مرتفعًا” (أكبر من أو يساوي ^6–10 مول/لتر) ، فإنه يتم حساب الرقم الهيدروجيني من خلال النظر فقط في ⁺H أو ^–OH المضافة.
2. عندما يكون التركيز “منخفضًا” (أقل من أو يساوي ^8–10 مول/لتر) ، يكون الرقم الهيدروجيني مساويا لـ 7.00. و هنا لم نقم بإضافة حمض أو قاعدة كافية لتغيير درجة حموضة الماء بحد ذاته.
3. عند التراكيز المتوسطة من ^6–10 مول/لتر إلى ^8–10 مول/لتر ، تكون تأثيرات تأين الماء والحمض أو القاعدة المضافة قابلة للمقارنة. فقط في هذه المنطقة يكون الحساب المنهجي للإتزان ضروريًا.

 

Water almost never produces 10^–7 M H⁺ and 10^–7 M OH^– , and that is true only in pure water with no added acid or base.

لا يمكن للماء العادي أن ينتج أيونات ⁺H تركيزها ^7–10 مول/لتر أو أيونات ^–OH تركيزها ^7–10 مول/لتر إلا إذا كان الماء نقيا جدا (مقطرا) و انه لم تتم إليه إيّ حمض أو قاعدة.

 

8 – 2  الحموض و القواعد الضعيفة

8 – 2 Weak Acids and Bases

Acid dissociation constant, K_a, for the acid HA, i.e. do not completely dissociate

ثابت تفكك الحمض K_a للحمض الضعيف HA ، أي بمعنى أن هذا الحمض لا يتفكك بالكامل :

Base dissociation constant, K_b, for the base B, i.e. do not completely dissociate

ثابت تفكك القاعدة K_b للقاعدة الضعيفة B، أي بمعنى أن هذه القاعدة لا تتفكك بالكامل :

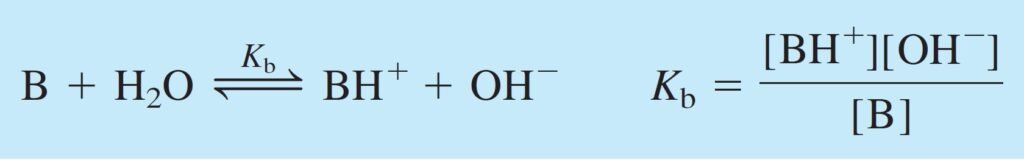
pK is the negative logarithm of an equilibrium constant:

pK هو اللوغاريتم السالب لثابت الإتزان

pK_w = –log K_w

pK_a = –log K_a

pK_b = –log K_b

As K increases, pK decreases, and vice versa. Comparing formic and benzoic acids, we see that formic acid is stronger, with a larger K_a and smaller pK_a, than benzoic acid.

كلما زادت قيمة K ، انخفضت قيمة pK ، والعكس صحيح. و بمقارنة حمض الفورميك مع حمض حمض البنزويك ، نجد بأن حمض الفورميك أقوى من حمض البنزويك حيث قيمة K_a لحمض الفورميك أكبر منها لحمض البنزويك.

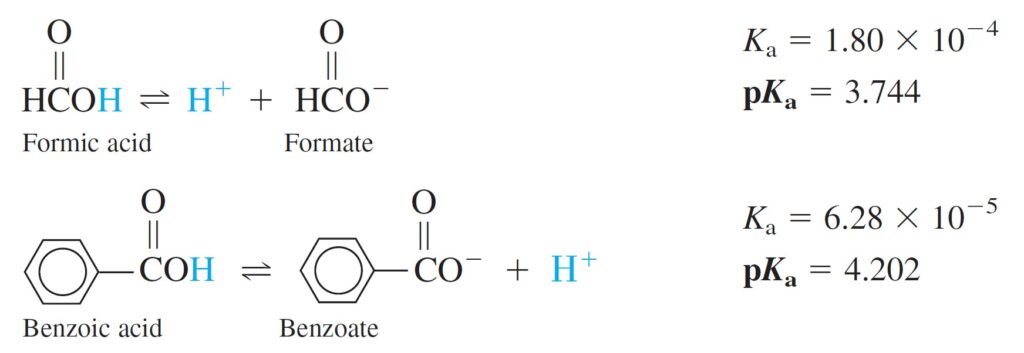
Conjugate base of a weak acid is a weak base.

القاعدة المرافقة للحمض الضعيف هي قاعدة ضعيفة.

Conjugate acid of a weak base is a weak acid.

الحمض المرافق للقاعدة الضعيفة هي حمض ضعيف.

Conjugate base of a strong acid is a very weak base or salt.

القاعدة المرافقة للحمض القوي هي قاعدة ضعيفة جدا أو ملحا ضعيف جدا .

Relation between K_a and K_b for conjugate pair:

العلاقة بين K_a و K_b للزوج المرافق

K_a . K_b = K_w         ……….. (5)

8 – 3  إتزان الحمض الضعيف

8 – 3  Weak-Acids Equilibria

Ortho-hydroxybenzoic acid is more acidic than para-hydroxybenzoic acid, because in ortho-hydroxybenzoic acid the product of the acid dissociation reaction can form a strong, internal hydrogen bond.

حمض أورثو هيدروكسي البنزويك (أورثو هيدروكسي حمض البنزويك) أكثر حمضية من حمض بارا هيدروكسي البنزويك لأنه في حمض أورثو هيدروكسي البنزويك يُمكن أن يشكل ناتج تفكك الحمض رابطة هيدروجينية داخلية قوية.

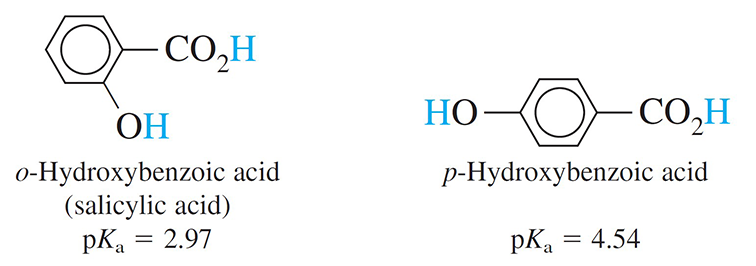
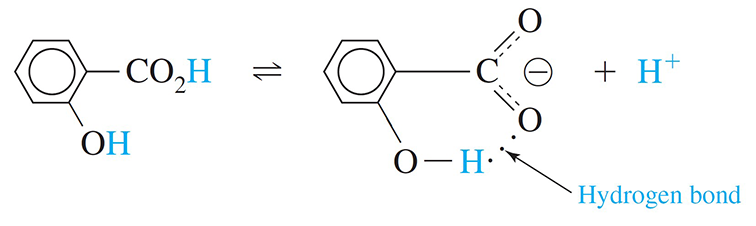
مسألة نموذجية عن الحمض الضعيف

A Typical Weak-Acid Problem

The problem is to find the pH of a solution of the weak acid HA, given the formal concentration of HA and the value of Ka. Let’s call the formal concentration F and use the systematic treatment of equilibrium:

تكمن المشكلة في إيجاد الرقم الهيدروجيني لمحلول الحمض الضعيف HA ، بالنظر إلى التركيز المثالي (أوالتركيز الرسمي) لـ HA وقيمة K_a. دعنا نرمز إلى التركيز الصيغي بالرمز F ونستخدم المعالجة المنهجية للإتزان.

Formal concentration is the total number of moles of a compound dissolved in a liter. The formal concentration of a weak acid is the total amount of HA placed in the solution, regardless of the fact that some has changed into A^–.

التركيز المثالي (أوالتركيز الرسمي) هو إجمالي عدد مولات المركب المذاب في اللتر. فالتركيز الصيغي (أو التركيز الرسمي) لحمض ضعيف هو إجمالي كمية HA الموجودة في المحلول ، بغض النظر عن حقيقة أن بعضها قد تغير إلى أيونات ^–A.

Step 1 Pertinent reactions.

الخطوة 1 التفاعلات ذات الصلة.

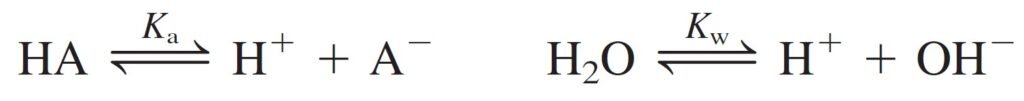
لاحظ هنا ان معادلة تفكك HA تُعد معادلة ذات صلة لأن HA تفكك جزئيا .

Step 2 The charge balance.

الخطوة 2 توازن الشحنة.

[H⁺] = [A^–] + [OH^–]          ……….. (6)

Step 3 Mass balance .

الخطوة 3 توازن الكتلة.

F = [A^–] + [HA]          ……….. (7)

Step 4 Equilibrium constant.

الخطوة 4 ثابت الاتزان .

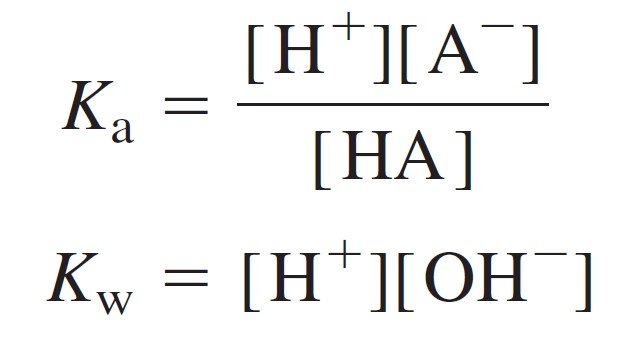……….. (8)

Step 5 Count the equations and unknowns. There are four equations and four unknowns ([H⁺], [OH^–], [AH], [A^–]), so we have enough information to solve the problem.

الخطوة 5 حساب و عد المعادلات و المجاهيل. هناك أربعة معادلات و أربعة مجاهيل ([⁺H], [^–OH], [AH], [^–A]) ، لذلك لدينا معلومات كافية لحل المسألة.

Step 6 Solve for all unknowns. Now, if dissociation of HA is much greater than dissociation of H₂O, then [A^–] >> [OH^–], and Equation 6 reduces to

الخطوة 6 حل كل المجاهيل. الآن ، إذا كان تفكك HA أكبر بكثير من تفكك H₂O ، فعندئذٍ سيكون تركيز [أA] أعلى بكثير من تركيز [^–OH] بحيث يتم تجاهل الأخير، و بالتالي تختصر المعادلة رقم 6 لتصبح :

[H⁺] ≈ [A^–]          ……….. (9)

To solve the problem, first set [H⁺] = x, and according to equation 9 we can say that [A^–] also is equal to x. Equation 7 says that [HA] =F – [A^–] = F – x. Putting these expressions into Equation 8 gives:

لحل هذه المسأله لنفترض من البداية أن تركيز [⁺H] يساوي x ، و طبقا للمعادلة رقم 7 فإنه باستطاعتنا القول أن تركيز [^–A] أيضا يساوي x . كما تخبرنا المعادلة 7 بأن:

[HA] =F – [A^–] = F – x

و بتعويض كل تلك القيم في المعادلة 8 نحصل على :

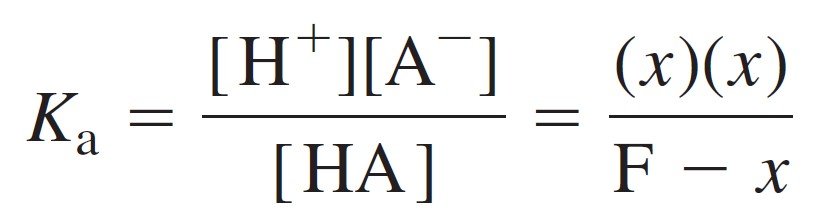
Setting F = 0.050 0 M and K_a = 1.07 × 10^–3 for o-hydroxybenzoic acid, we can solve the equation, because it is just a quadratic equation.

The calculated pH is 2.17, which means that [OH^–] = K_w/[H⁺] = 1.5 × 10^–12 M.

Fraction of Dissociation التفكك الجزئي

The fraction of dissociation, α, is defined as the fraction of the acid in the form A^–

التفكك الجزئي و يرمز له بالرمز ألفا α ،و يعرف التفكك الجزئي بأن التفكك الجزئي للحمض على شكل أيونات ^–A .

For 0.050 0 M o-hydroxybenzoic acid, we find

و لمحلول حمض أورثو هيدروكسي البنزويك تركيزه 0.050 مول/لتر ، فإن التفكك الجزئي يساوي :

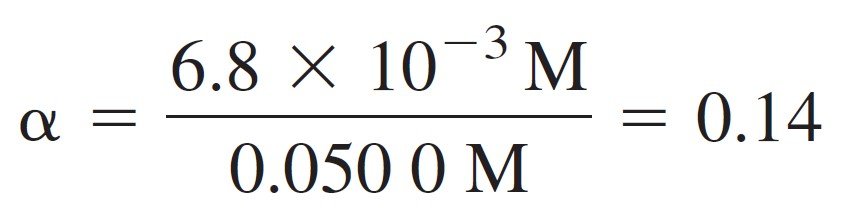
That is, the acid is 14% dissociated at a formal concentration of 0.050 0 M.

و هذا يعني أن حمض أورثو هيدروكسي البنزيك يتفكك بنسبة 14% عندما يبكون تركيزه الصيغي (أو تركيزه الرسمي) يساوي 0.050 مول/لتر .

 

The Essence of a Weak-Acid Problem

When faced with finding the pH of a weak acid, you should immediately realize that:

عندما يطلب منك إيجاد الرقم الهيدروجيني لحمض ضعيف ، يجب أن تدرك على الفور أن :

[H⁺] = [A^–] = x  

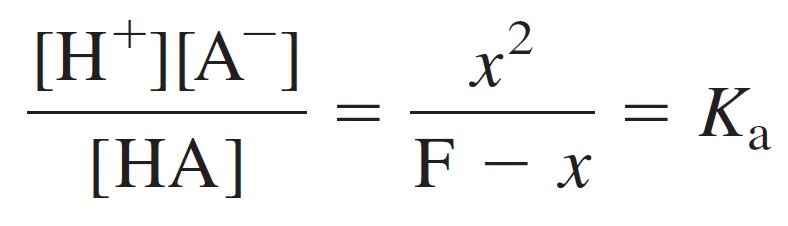
8 – 4  إتزان القاعدة الضعيفة

8 – 4  Weak-Base Equilibria

The treatment of weak bases is almost the same as that of weak acids.

إن معالجة القواعد الضعيفة على الأغلب تشبه الطريقة نفسها للحموض الضعيفة

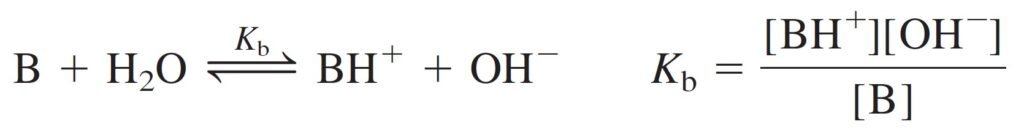
We suppose that nearly all OH^– comes from the reaction of B + H₂O, and little comes from dissociation of H₂O. Setting [OH^–] = x, we must also set [BH⁺] = x, because one BH⁺ is produced for each OH^–. Calling the formal concentration of base F (= [B] + [BH⁺]), we write:

هنا نفترض أن تقريبا جميع أيونات ^–OH جاءت من تفاعل B + H₂O و أن القليل من تلك الأيونات جاءت من تفكك H₂O . و بافتراض أن [^–OH] تساوي x ، فإنه يمكننا القول أن [⁺BH] تساوي x  أيضا، لأن مقابل كل ⁺BH يتم انتاجها يتم انتاج  ^–OH . و حيث أن التركيز الصيغي (أو التركيز الرسمي) F للقاعدة يساوي [B] + [⁺BH] فإنه يمكننا أن نكتب :

Plugging these values into the K_b equilibrium expression, we get

و بتعويض كل تلك القيم  في معادلة K_b ، نحصل على :

 

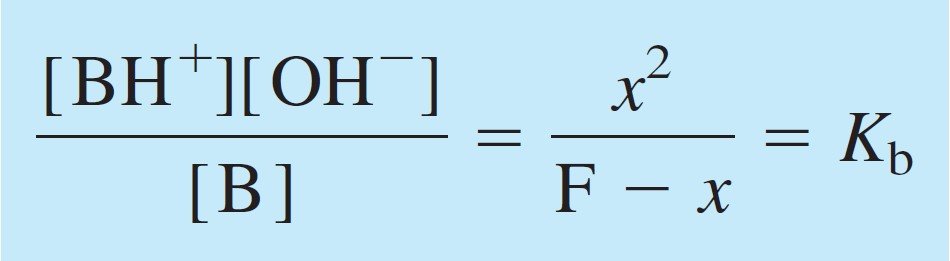
 مسألة قاعدة ضعيفة نموذجية A Typical Weak-Base Problem

If we consider the formal concentration of Cocaine is 0.0372 M, K_b is 2.6×10^–6 the problem can be solved as follows:

لو افترضنا أن التركيز الصيغي للكوكائين هو 0.0372 مول/لتر، و Kb تساوي ^6–10×2.6 فإنه يمكن حل المسألة كما ياـي :

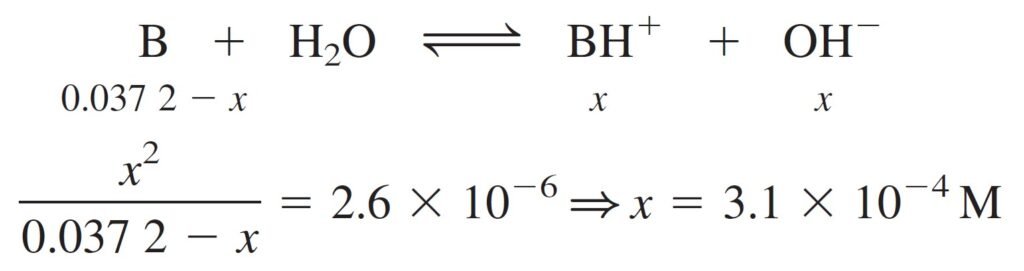
Because x = [OH^–], we can write:

و لكون [^–OH] تساوي x ، فإنه يمكننا كتابة :

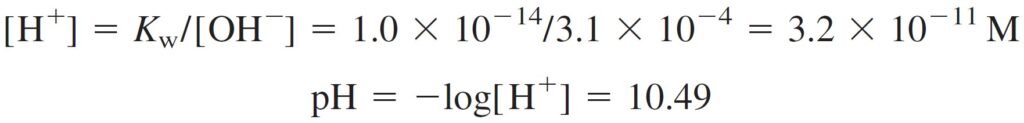
We can formulate (alpha α ) for a base, called the fraction of association:

يمكننا الأن صياغة (alpha α) للقاعدة تسمى الارتباط التجزيئي:

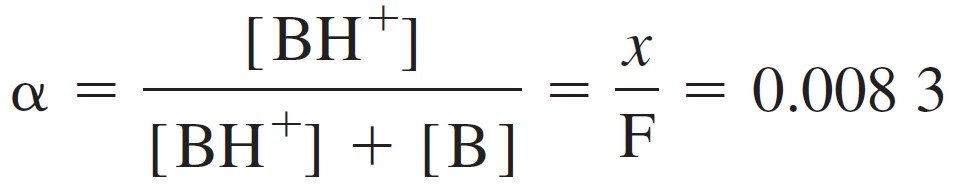
8 – 5  المحاليل المنظمة

8 – 5  Buffers

A Buffered solution is one that resists a change in its pH when either hydroxide ions or protons are added.

المحلول المنظم هو المحلول الذي يقاوم التغير في الرقم الهيدروجيني pH عند إضافة أيونات الهيدروكسيد أو البروتونات إليها.

Buffered solution may contain a weak acid and its conjugate base (for example, HF and NaF) or a weak base and its conjugate acid(for example, NH₃ and NH₄Cl).

قد يحتوي المحلول المنظم على حمض ضعيف و قاعدته المرافقة (مثلا: HF و NaF) ، أو قاعدة ضعيفة و حمضها المرافق (مثلا: NH₃ و NH₄Cl) .

If you mix A moles of a weak acid with B moles of its conjugate base, the moles of acid remain close to A and the moles of base remain close to B.

إذا قمت بخلط عددا من مولات الحمض الضعيف A مع عددا من مولات قاعدة الحمض المرافقة B ، فإن مولات الحمض تظل قريبة من A وتظل مولات القاعدة قريبة من B. أي انه لا يحدث هناك أي تغير يذكر في عدد المولات أو التركيز في كلا المادتين .

Consider an acid with pK_a = 4.00 and its conjugate base with pK_b = 10.00. Calculate the fraction of acid that dissociates in a 0.10 M solution of HA.

افترض أن هناك حمض قيمة الـ pKa له تساوي 4.00 ، و قيمة الـ pKb لقاعدته المرافقة تساوي 10.00 ، احسب كمية الحمض التي تفككت في محلول HA (أي: محلول حمضي) تركيزه 0.10 مول/لتر .

Now, consider adding 0.10 M of conjugate base with pK_b = 10.00 .

الان ، افترض أننا قمنا بإضافة قاعدة مرافقة تركيزها 0.10 مول/لتر و قيمة pK_b لها تساوي 10.00

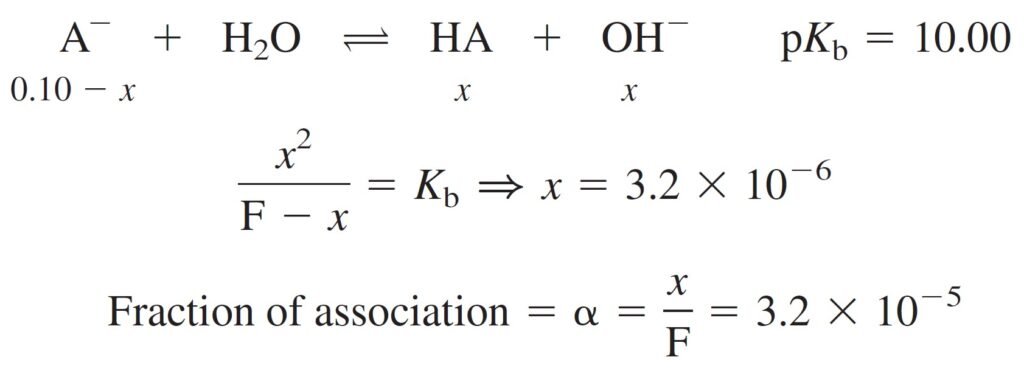
We can noticed that HA dissociates very little, and adding extra A^– to the solution makes HA dissociate even less. Similarly, A^– does not react much with water, and adding extra HA makes A^– react even less.

يمكننا أن نلاحظ أن الحمض HA يتفكك قليلاً جدًا ، و إن إضافة A- إلى المحلول يجعل HA تفكك بشكل أقل أيضا . وبالمثل ، لا تتفاعل القاعدة المرافقة  ^–A كثيرًا مع الماء ، وإضافة المزيد من الحمض HA تجعل تفاعل ^–A أقل.

 

Henderson-Hasselbalch Equation معادلة هندرسون-هاسلبالخ

The central equation for buffers is the Henderson-Hasselbalch equation, which is merely a rearranged form of the Ka equilibrium expression.

إن المعادلة الرئيسة للمحاليل المنظمة هي معادلة هندرسون-هاسلبالخ Henderson-Hasselbalch equation، وهي مجرد شكل معاد ترتيبه من قانون الإتزان K_a.

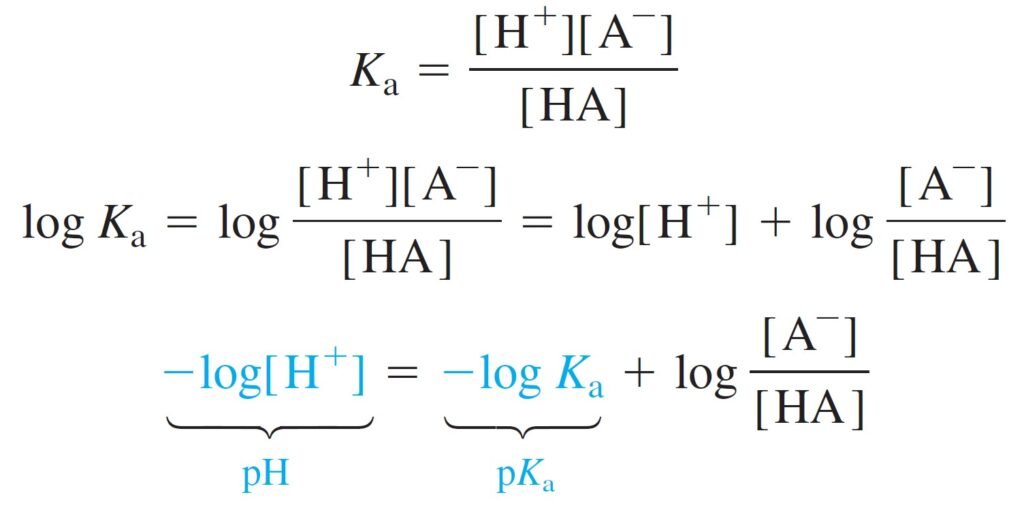
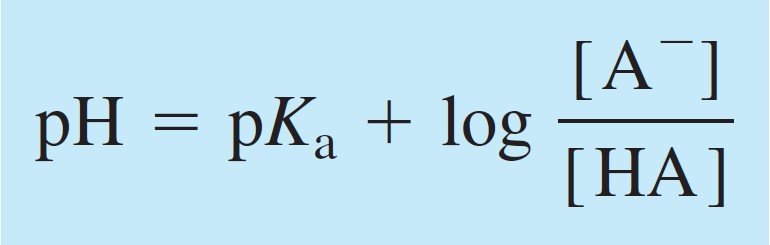
We can calculate the pH of the solution using Henderson-Hasselbalch equation if we know the ratio of the concentrations of conjugate acid and base, as well as pK_a for the acid.

يمكننا حساب الرقم الهيدروجيني للمحلول باستخدام ممعادلة هندرسون-هاسلبالخ إذا عرفنا نسبة تركيزات الحمض والقاعدة المرافقة، وكذلك pK_a للحمض.

If [A^–] = [HA] , pH = pKa

All equilibria must be satisfied simultaneously in any solution at equilibrium

Only one concentration of H+ in a solution

If a solution is prepared from the weak base B and its conjugate acid, the analogous equation is

إذا تم تحضير محلول من القاعدة الضعيفة B وحمضها المرافق، فإن المعادلة تصبح :

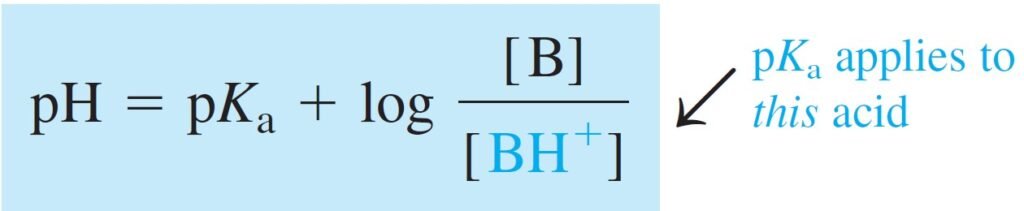
where pK_a is the acid dissociation constant of the weak acid BH⁺.

حيث pK_a ثابت تفكك الحمض للحمض الضعيف ⁺BH .

Example4 :  Calculate the pH of a solution containing 0.75 M lactic acid (K_a = 1.4×10^-4) and 0.25 M sodium lactate.

مثال4 : أحسب الرقم الهيدروجيني pH لمحلول يتكون من حمض اللاكتيك  تركيزه 0.75 مول/لتر (K_a = 1.4×10^-4) و أيضا على لاكتات الصوديوم  تركيزه 0.25 مول/لتر .

Solution: 

نستطيع أن نستخدم معادلة هندرسون-هاسلبالخ

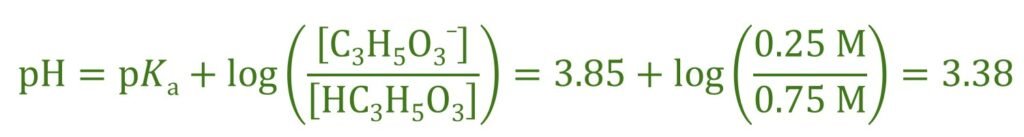
المصادر:

• Quantitative Chemical Analysis by Daniel C. Harris, 8th Edition
• الموسوعة العلمية الكيميائية للأستاذ أكرم العلي

بوسترات (لوحات) كيميائية بدقة عالية (أكثر من 25 لوحة) من تصميم الأستاذ أكرم أمير العلي

 

تطبيقات كيميائية من تصميم الأستاذ أكرم امير العلي متوفر للجوالات التي تعمل بنظام أندرويد android على سوق جوجل بلاي google play

1 – تطبيق ملصقات الجدول الدوري باللغة العربية : بطاقات تحتوي على معلومات شاملة و مختصرة في نفس الوقت كل عنصر على حدة (اللغة العربية).

https://play.google.com/store/apps/details?id=com.akramir2

مقالات قد تفيدك :