إتزان الحمض – القاعدة عديدة البروتون
Polyprotic Acid-Base Equilibria
( Sections 9.1 – 9.6, Quantitative Chemical Analysis by Daniel C. Harris, 8th Edition )
( التحليل الكيميائي النوعي – دانيال هاريس )
Polyprotic systems: Acid or bases that can donate or accept more than one proton.
الأنظمة متعددة أو عديدة البروتون : حموض أو قواعد يمكنها أن تمنج أو تستقبل أكثر من برونون واحد .
Proteins are a common example of a polyprotic system.
فالبروتينات مثلا هي مثال واضح على الأنظمة متعددة أو عديدة البروتون.
9 – 1 الحموض و القواعد ثنائية البروتون
9 – 1 Diprotic Acids and Bases
Amino acids from which proteins are built have an acidic carboxylic acid group, a basic ammonium group, and a variable substituent designated R.
تتكون الحموض الأمينية (الأحماض الأمينية) التي تُبنى منها البروتينات على مجموعة كربوكسيل حمضية ، و مجموعة أمونيوم قاعدية، و مجموعة بديلة متغيرة تسمى R.

Carboxyl group is stronger acid of ammonium group.
مجموعة الكربوكسيل حمض قوي مقارنة مع مجموعة الأمونيوم.
R is different group for each amino acid.
مجموعة R تختلف باختلاف الحمض الأميني.
Amino acids are zwitterion – molecule with both positive and negative charge.
الحموض الأمينية هي زويتريونات (جزيئات متعادلة أو أيونات مزدوجة)، أيّ: يجزيء يحوي على شحنة سالبة و شحنة موجبة في نفس الوقت.
At low pH, both ammonium and carboxy group are protonated.
عندما تكون قيمة الرقم الهيدروجيني pH منخفضة فإنه يمكن في هذه الحالة إضافة البروتون إلى كل من مجموعة الكربوكسيل و مجموعة الأمونيوم.
At high pH, neither group is protonated.
أما عندما تكون قيمة الرقم الهيدروجيني مرتفعة فإنه لا يحدث إضافة للبروتون إلى كل من مجموعة الكربوكسيل و مجموعة الأمونيوم.
Zwitterions are stabilized in solution by interactions of ammonium ion and carboxylic acid with water.
يمكن أن نجعل الزويتريونات أكثر استقرارا في المحلول من خلال التحكم في تفاعلات محموعة الأمونيوم و مجموعة الكربوكسيل مع الماء.
Lets take amino acid leucine, designated HL as an example.
لنأخذ الحمض الأميني ليوسين و الذي يرمز له بالرمز HL كمثال.
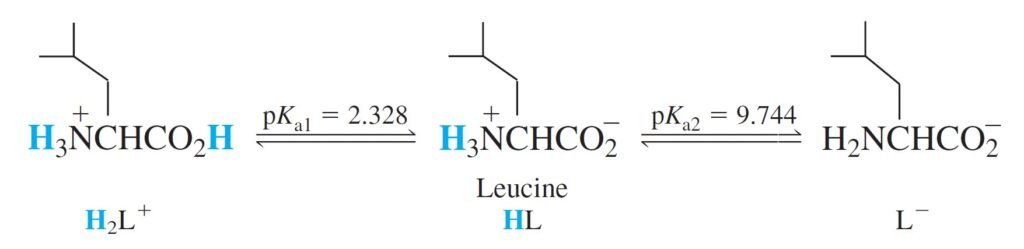
The equilibrium constants refer to the following reactions
كما تشير ثوابت الاتزان للتفاعلات الآتية:
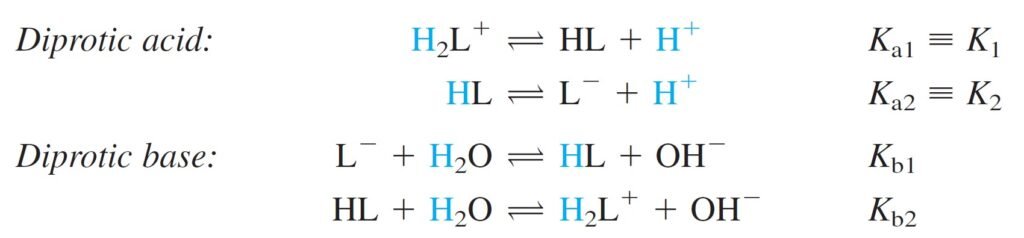
Remember that the relations between the acid and base equilibrium constants are:
وتذكر أن العلاقة بين ثابت الإتزان للحمض مع ثابت الإتزان للقاعدة كما يأتي:
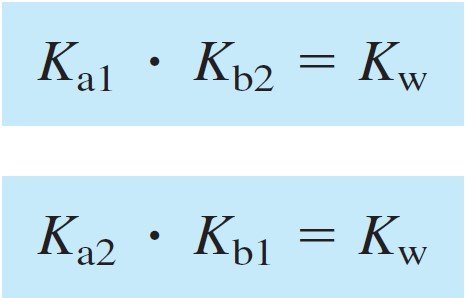
Lets calculate the pH and composition of individual solutions of 0.050 M H2L+ (Acid form), 0.050 M HL (Intermediate form), and 0.050 M L– (Basic form).
The Acidic Form, H2L+ الصيغة الحمضية
H2L+, can dissociate twice as shown above.
يمكن للحمض +H2L أن يتفكك على خطوتين، كما هو مبين أعلاه.
Because K1 = 4.70 × 10–3, H2L+ is a weak acid and HL is an even weaker acid, because K2 = 1.80 × 10–10.
و حيث أن قيمة K1 للحمض +H2L تساوي 3–10× 4.70 ، فإن هذا الحمض بالتأكيد يمكن أن يُعد حمضا ضعيفا. كما يمكن أن يعد الحمض HL حمضا ضعيفا جدا لأن قيمة K2 الخاصة به تساوي 10–10× 1.80 .
It appears that the H2L+ will dissociate only partly, and the resulting HL will hardly dissociate at all. For this reason, we make the approximation that a solution of H2L+ behaves as a monoprotic acid, with Ka = K1, and hence finding the pH of 0.050 M H2L+ is easy.
و هنا يتبين أن الحمض +H2L سوف يتفكك جزئيا فقط ، و لطالما أن الحمض النتاج عن تفككه و الذي هو HL صعب جدا أن يتفكك، فلهذا السبب يمكن أن نفترض بأن محلول الحمض +H2L يمكن أن يسلك سلوك الحموض الأحادية البروتون حيث Ka تساوي K1 ، و بالتالي يسهل إيجاد قيمة الرقم الهيدروجيني pH للحمض +H2L ذو التركيز 0.050 مول/لتر .
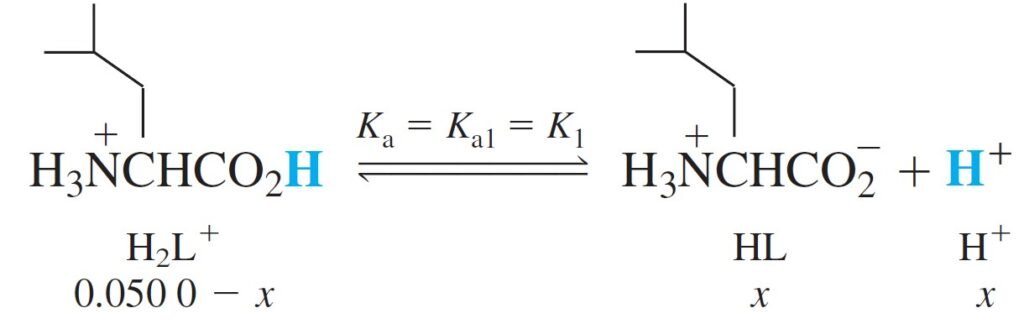
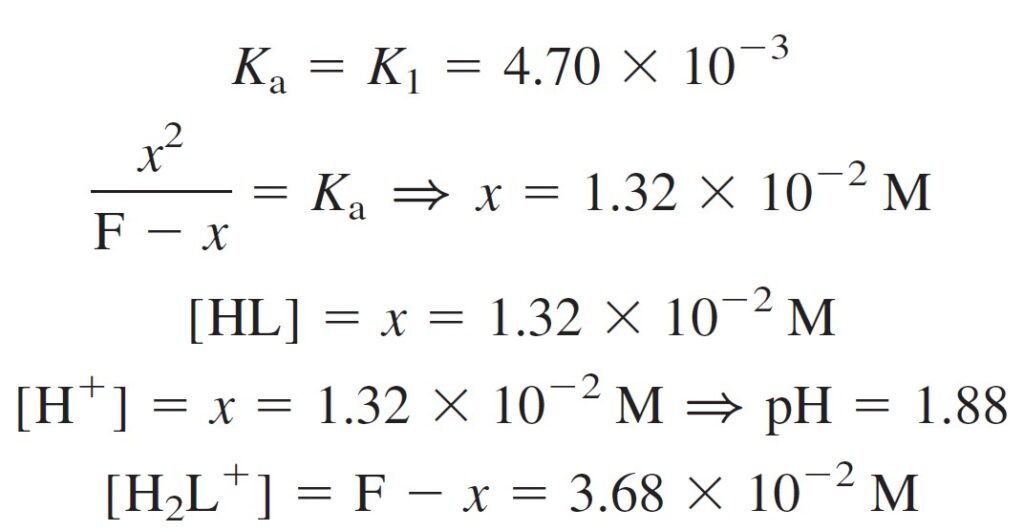
From the above calculations we find:
من الحسابات أعلاه نجد بأن:
[HL] = [H+] = 1.32 × 10–2
[H2L+] = 3.68 × 10–2
Now, what is the concentration of L– in the solution? In the fact it is very small, but not zero, and it will be calculated from K2.
و الآن، ما هو تركيز –L في المحلول؟ في الحقيقة إن تركيز –L قليل للغاية، و لكن لن تصل إلى درجة “صفر” و يمكن حسابها من K2 .
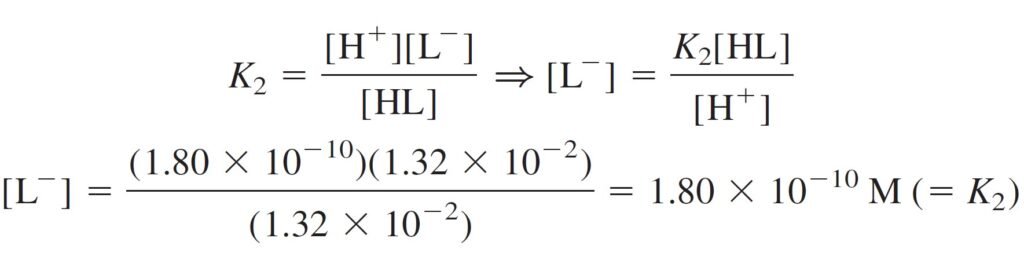
For most diprotic acids, K1 is sufficiently larger than K2.
لأغلب الحموض ثنائي البروتون، فإن قيمة K1 تكون أعلى بكثير من قيمة K2 .
In summary, a solution of a diprotic acid behaves like a solution of a monoprotic acid, with Ka = K1.
باختصار محلول الحمض ثنائي البروتون يسلك سلوك المحلول أحادي البروتون حيث Ka تساوي K1 .
The Basic Form, L– الصيغة القاعدية
Sodium leucinate, can be prepared by treating leucine (HL) with an equimolar quantity of NaOH.
يمكن تحضير ليوسينات الصوديوم عن طريق تفاعل الليوسين HL مع كمية متساوية موليا من هيدروكسيد الصوديوم NaOH .
Dissolving sodium leucinate in water gives a solution of L–.
تذويب ليوسينات الصوديوم في الماء يعطي محلولا يحتوي على أيونات –L :
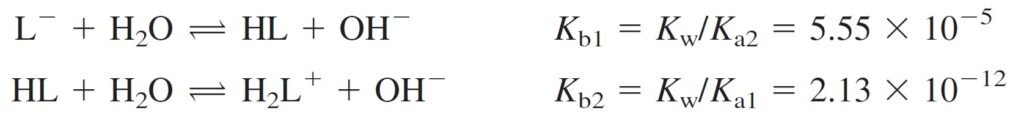
Because Kb1 = 5.55 × 10–5, L– is a weak base and HL is an even weaker base , because Kb2 = 2.13 × 10–12.
و حيث أن قيمة Kb1 للقاعدة –L تساوي 5–10× 5.55 ، فإن هذه القاعدة بالتأكيد يمكن أن تعد قاعدة ضعيفة. كما يمكن أن تعد HL قاعدة ضعيفة جدا لأن قيمة Kb2 الخاصة بهh تساوي 12–10× 2.13 .
Now, what is the pH of 0.050 M Leucine salt (Sodium leucinate, L– ) ?
الآن ما هي قيمة الرقم الهيدروجيني pH لمحلول ملح الليوسين (ليوسينات الصوديوم) تركيزه 0.050 مول/لتر ؟
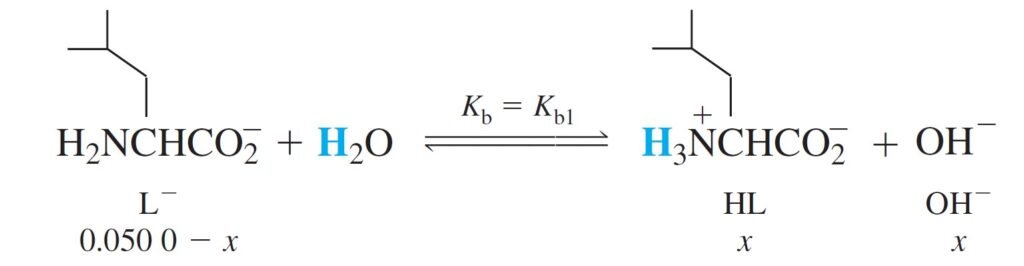
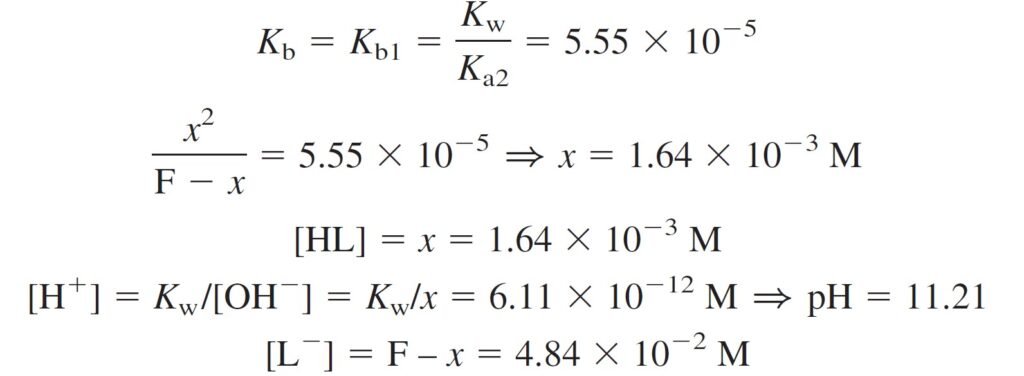
The concentration of H2L+ can be found from the Kb2 (or Ka1) equilibrium.
و يمكن حساب تركيز +H2L من Kb2 أو من Ka1 .
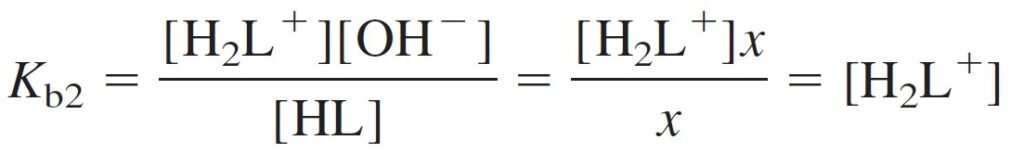
[H2L+] = 2.13 × 10–12 is very smaller than [HL] = 1.64 × 10–3
Fully basic form of a diprotic acid can be treated as a monobasic, Kb=Kb1
من الحسابات أعلاه يمكننا القول أن الشكل القاعدي من الحمض ثنائي البروتون يسلك سلوك الشكل آحادي القاعدية حيث Kb يساوي Kb1 .
The Intermediate Form, HL الصيغة الوسطية
A solution prepared from leucine, HL, is more complicated because HL is both an acid and a base and it said to be amphiprotic.
المحلول HL المحضر من الليوسين اكثر تعقيدا ، لأن HL حمض و قاعدي في نفس الوقت و يطلق عليه اسم امفوتيري أو متردد.
A molecule that can both donate and accept a proton is said to be amphiprotic.
الجزيء الذي يمكنه منح و استقبال بروتون يعرف باسم أمفوتيري او متردد .
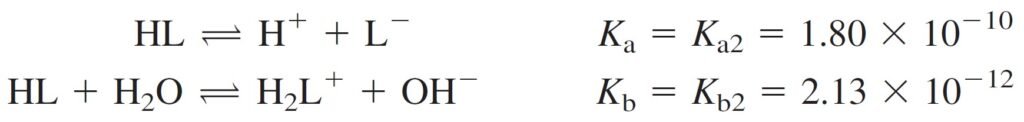
Since Ka > Kb, expect to be acidic, and in same time we can not ignore Kb.
من القراءات أعلاه، نجد بأن Ka أكبر من Kb ، و بالتالي يتوقع أن يكون المحلول حمضيا ، و بنفس الوقت لا يمكننا تجاهل Kb .
Both reactions proceed to nearly equal extent, because H+ produced in the above first reaction reacts with OH– produced in the second reaction, thereby driving the second reaction to the right.
فكلا التفاعلين الظاهرين أعلاه يحدثان إلى حد متساوٍ تقريبًا ، لأن أيونات +H الناتجة من التفاعل الأول تتفاعل مع أيونات –OH الناتجة من التفاعل الثاني و هذا يدفع التفاعل الثاني للسير جهة اليمين.
To treat this case, we resort to the systematic treatment of equilibrium.
لمعالجة هذه الحالة ، نلجأ إلى المعالجة المنهجية للإتزان.
- Step 1 Pertinent reactions:
الخطوة 1 التفاعلات ذات الصلة.
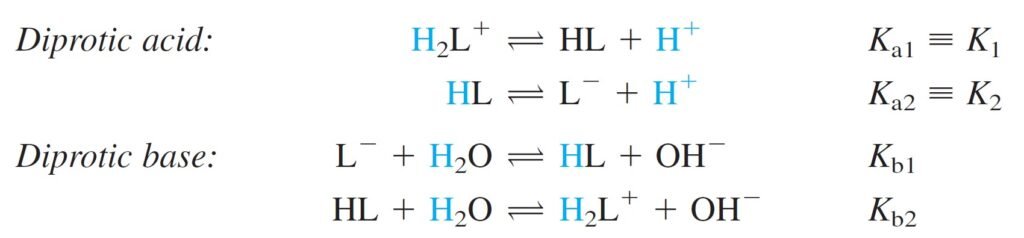
- Step 2 Charge balance:
الخطوة 2 توازن الشحنة.
[H+] + [H2L+] = [OH–] + [L–]
OR
[H2L+] – [L–] + [H+] – [OH–] = 0
- Step 3 Mass balance
الخطوة 3 توازن الكتلة.
F = [HL] + [H2L+] + [L–]
- Step 4 equilibrium constant expression for each chemical reaction.
الخطوة 4 معادلة الثابت الاتزان لكل تفاعل كيميائي.
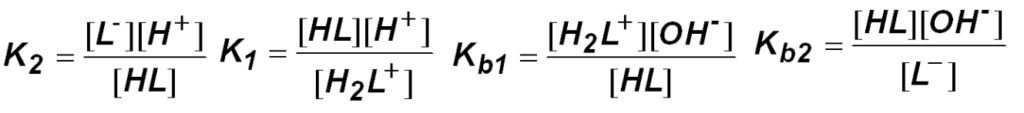
- Step 5 Count the equations and unknowns. We have 4 unknowns.
الخطوة 5 حساب و عد المعادلات و المجاهيل. لدينا أربعة مجاهيل.
- Step 6 Solve for all unknowns.
الخطوة 6 حل كل المجاهيل.
Since :
[H2L+] = [HL][H+]/K1
[L–] = [HL]K2/[H+]
[OH–] = Kw/[H+]
Putting these expressions into the charge balance gives:
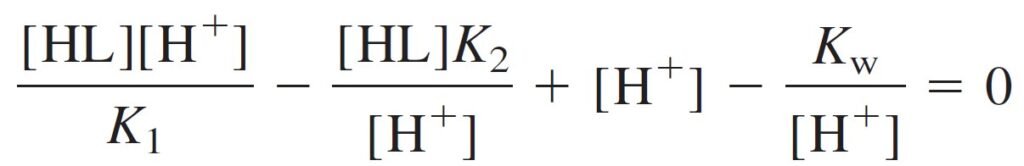
which can be solved for [H+]. First, multiply all terms by [H+]:
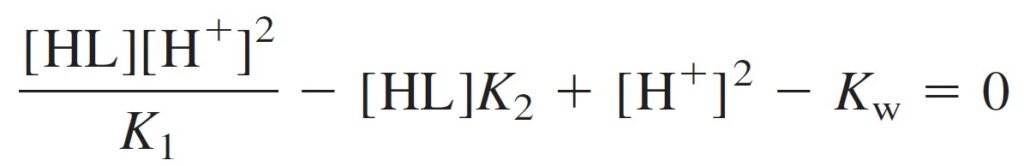
Then rearrange and factor out [H+]2:
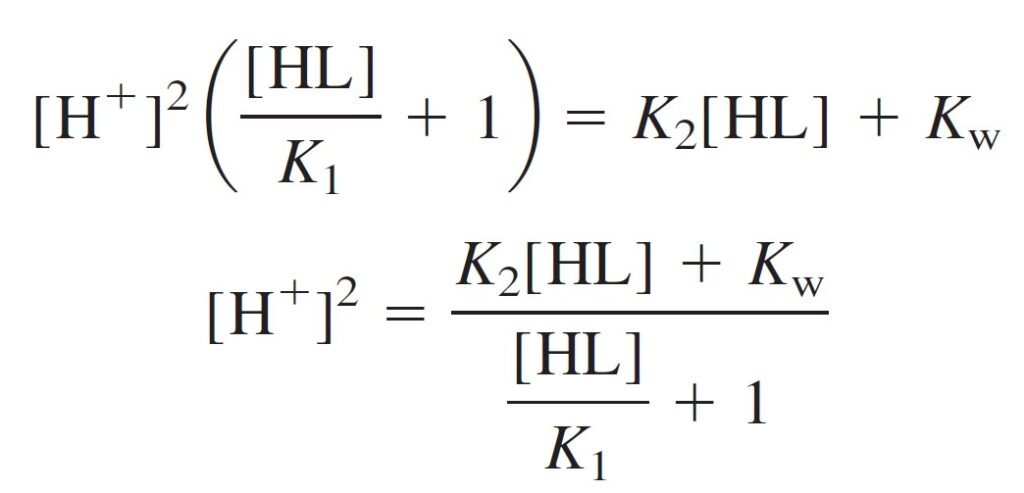
Now multiply the numerator and denominator by K1 and take the square root:
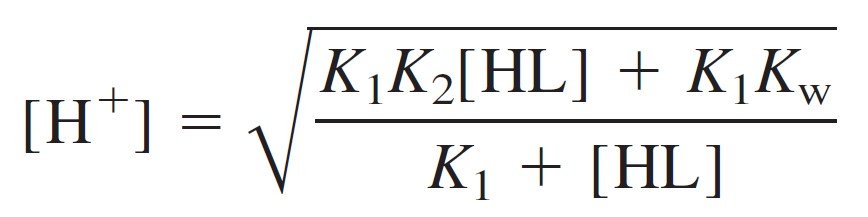
For [HL] in the above equation we can simply substitute the formal concentration, 0.050 0 M.
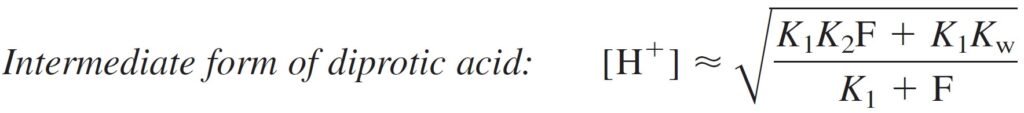
where F is the formal concentration of HL (= 0.050 M in the present case). At long last, we can calculate the pH of 0.050 M leucine:
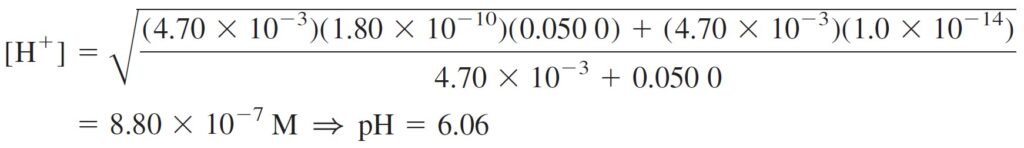
The concentrations of H2L+ and L– can be found from the K1 and K2 equilibria, using [H+] = 8.80 × 10–7 M and [HL] = 0.050 M.
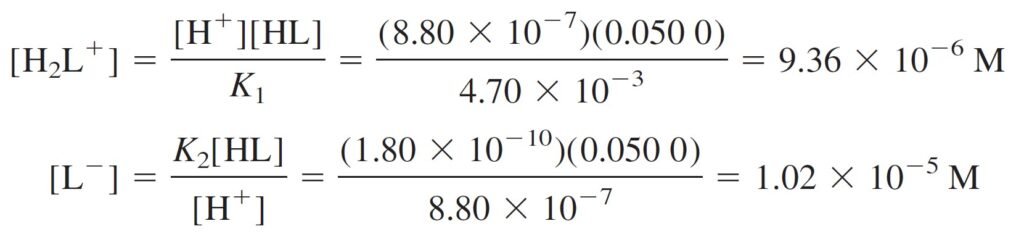

حسابات مبسطة للصيغة الوسطية
Simplified Calculation for the Intermediate Form
The following equation can be simplified further to calculate intermediate form:
المعادلة الآتية يمكن تبسيطها أكثر لحل الصيغة الوسطية:
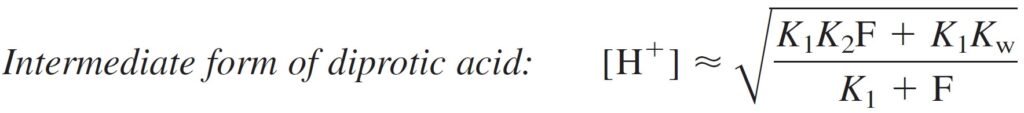
if K2F >> Kw, then K1Kw can be dropped from numerator:
إذا كان K2F أكبر بكثير من Kw ، فإنه يمكن حذف K1Kw من البسط فتصبح المعادلة :
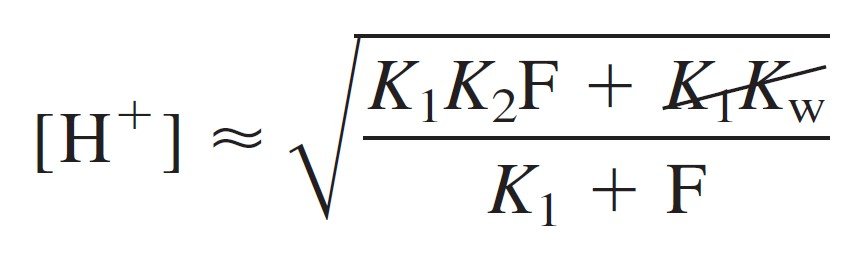
Then, if K1 << F, the first term in the denominator also can be neglected.
و أيضا، إذا كان K1 أصغر بكثير من F فإنه يمكن حذفها من المقام:
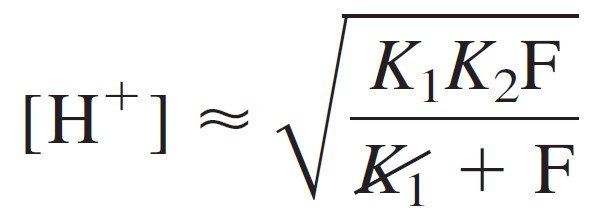
Canceling F in the numerator and denominator gives
وحذف F من البسط و المقام يعطينا
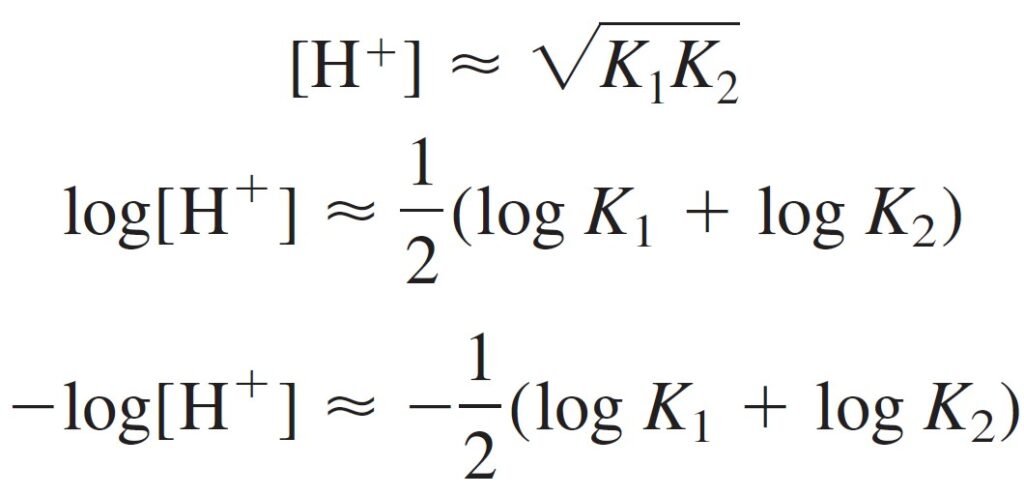
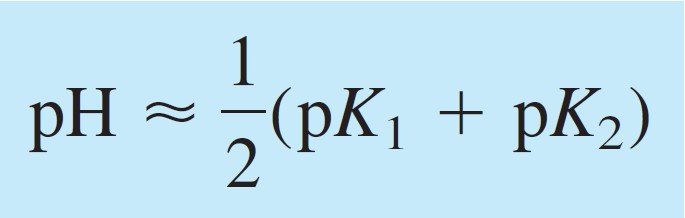
The pH of the intermediate form of a diprotic acid is close to midway between pK1 and pK2, regardless of the formal concentration.
يكون الرقم الهيدروجيني للصيغة الوسطية لحمض ثنائي البروتون قريبًا من منتصف المسافة بين pK1 و pK2 ، بغض النظر عن التركيز الصيغي (أو الرسمي) .
9 – 2 المحاليل المنظمة ثنائية البروتون
9 – 2 Diprotic Buffers
A buffer made from a diprotic (or polyprotic) acid is treated in the same way as a buffer made from a monoprotic acid.
يتم التعامل مع المحلول المنظم المحضر من حمض ثنائي البروتون (أو عديد البروتونات) بنفس طريقة التعامل مع المحلول المنظم المحضر من حمض أحادي البروتون.
For the acid H2A, we can write two Henderson-Hasselbalch equations, both of which are always true.
بالنسبة للحمض H2A ، فإنه يمكننا كتابة معادلتي هندرسون-هاسيلباخ ، وكلاهما صحيح .
Choice of equation is based on what is known:
- – If [H2A] and [HA–] known, use pK1 equation.
- – If [HA–] and [A2–] known, use pK2 equation.
فاختيار المعادلة الانسب للحل يعتمد على ما هو معلوم للحل:
- فإذا كان معلوما لديك [H2A] و [–HA] ، فاستخدم معادلة pK1 .
- فإذا كان معلوما لديك [–HA] و [–A2] ، فاستخدم معادلة pK2 .
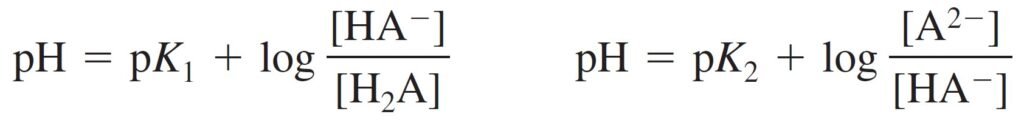
9 – 3 الحموض و القواعد عديدة البروتون
9 – 3 Polyprotic Acids and Bases
The treatment of diprotic acids and bases can be extended to polyprotic systems.
يمكن أن تمتد معالجة الحموض والقواعد ثنائية البروتون إلى الأنظمة متعددة اليروتونات.
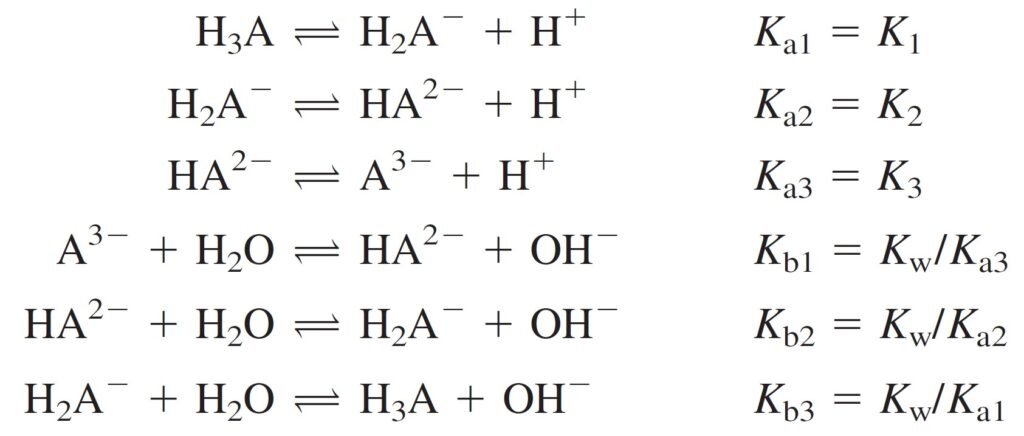
We deal with triprotic systems as follows:
نتعامل مع الأنظمة ثلاثية البروتونات كما يأتي:
1 – H3A is treated as a monoprotic weak acid, with Ka = K1.
1 – يتم التعامل مع H3A و كأنه حمض ضعيف أحادي البروتون، حيث Ka تساوي K1 .
2 – H2A– is treated as the intermediate form of a diprotic acid.
2 – يتم التعامل مع –H2A و كأنه صيغة وسطية لحمض ثنائي البروتون .

OR pH = ½(pK1+pK2)
3 – HA2– is treated as the intermediate form of a diprotic acid.
3 – يتم التعامل مع –HA2 و كأنه صيغة وسطية لحمض ثنائي البروتون .
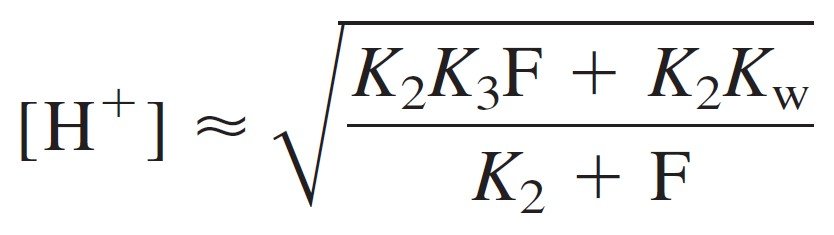
OR pH = ½(pK2+pK3)
4 – A3– is treated as monobasic, with Kb = Kb1 = Kw / Ka3.
4 – يتم التعامل مع –A3 و كأنها قاعدة أحادية البروتون حيث Kb تساوي Kb1 تساوي Kw / Ka3 .
9 – 4 ما هي الدقائق أو الجسيمات السائدة؟
9 – 4 Which is the principal Species?
We sometimes must identify which species of acid, base, or intermediate predominates under given conditions.
قد يلزم أحيانا أن نحدد أي الجسيمات أو الدقائق الحمضية أو القاعدية أو الوسطية هي السائدة في طل ظروف معينة.
For a monoprotic system, the basic species A– is the predominant form when pH > pKa. The acidic species, HA, is the predominant form when pH < pKa.
بالنسبة للنظام أحادي البروتون، فإن الجسيمات أو الدقائق القاعدية –A هي الشكل السائد عندما يكون الرقم الهيدروجيني pH أكبر من pKa. و تكون الجسيمات أو الدقائق الحمضية HA ، هي الشكل السائد عندما يكون الرقم الهيدروجيني pH أصغر من pKa.
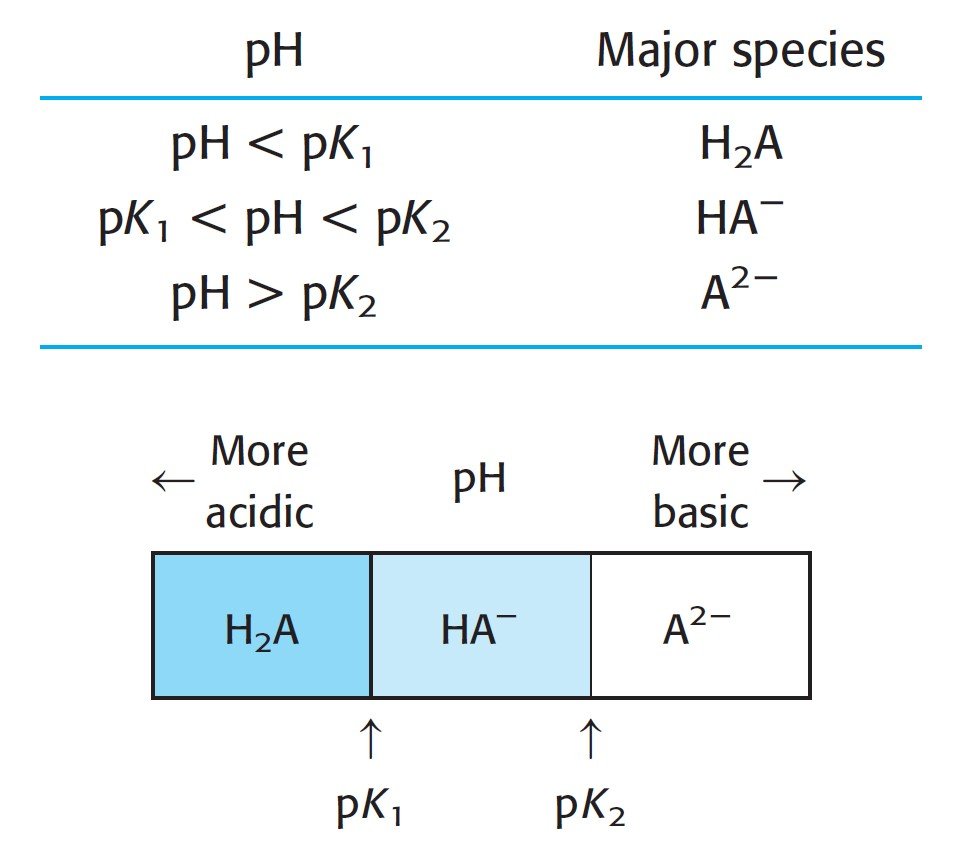
The following figure summarizes how determine the predominant form in case of diprotic system. We determine the principal species by comparing the pH of the solution with the pKa values.
يلخص الشكل الأتي كيفية تحديد الشكل السائد في حالة النظام ثنائي البروتون. فنحن نحدد الأنواع الرئيسة من خلال مقارنة الرقم الهيدروجيني للمحلول مع قيم pKa.
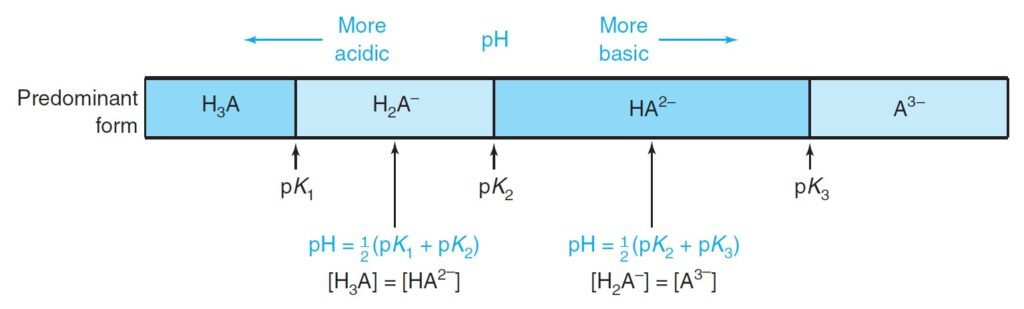
The following figure summarizes how determine the predominant form in case of triprotic system. We determine the principal species by comparing the pH of the solution with the pKa values.
يلخص الشكل الأتي كيفية تحديد الشكل السائد في حالة النظام ثلاثي البروتون. فنحن نحدد الأنواع الرئيسة من خلال مقارنة الرقم الهيدروجيني للمحلول مع قيم pKa.
9 – 5 معادلات التركيب الجزئي
9 – 5 Fractional Composition Equations
These equations will be useful for acid-base and EDTA titrations, as well as for electrochemical equilibria.
هذه النعادلات مفيدة في حالات معايرات الحمض-القاعدة و معايرات EDTA بالإضافة إلى الإتزانات أو التوازنات الكهروكيميائية.
Monoprotic System الأنظمة أحادية البروتون
Find an expression for the fraction of an acid in each form (HA and A–) as a function of pH.
الهدف هنا إيجاد معادلة للتفكك الجزئي للحمض لكل شكل HA و –A بدلالة الرقم الهيدروجيني.
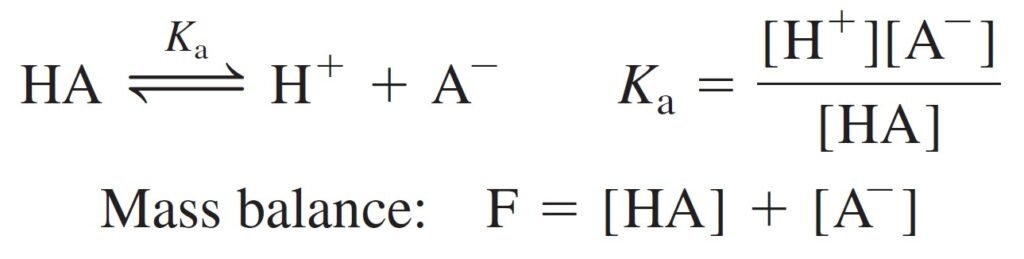
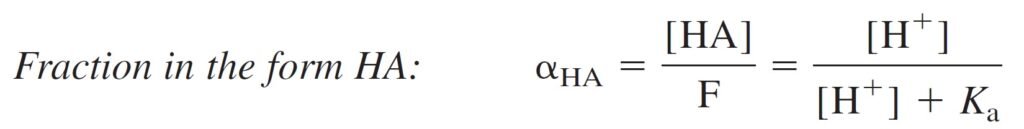
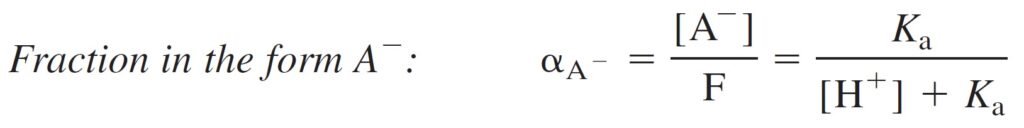
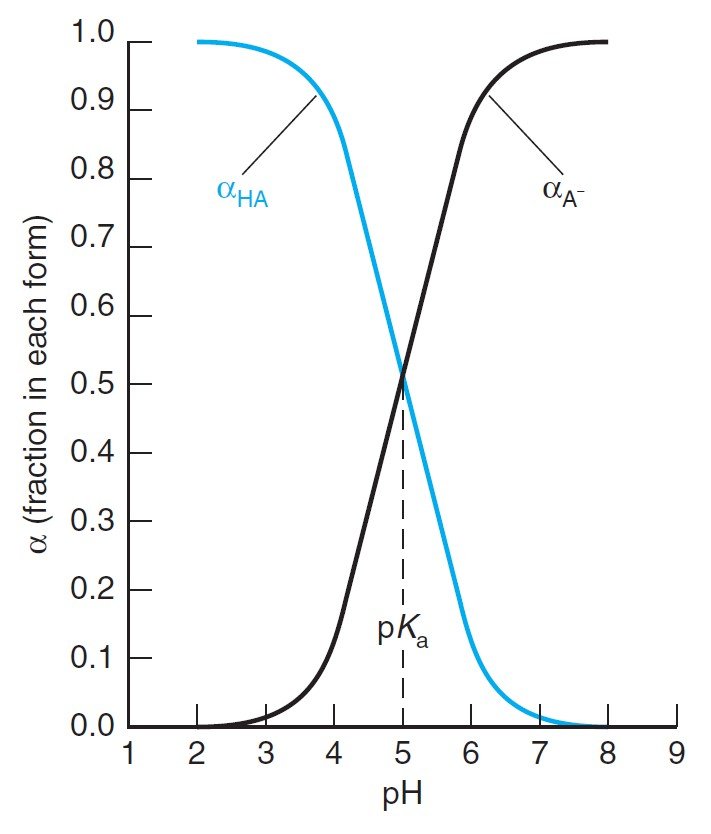
Below figure shows αHA and αA– for a system with pKa = 5.00. At low pH, almost all of the acid is in the form HA. At high pH, almost everything is in the form A–.
يوضح الشكل أدناه قيم αHA و–αA لنظام قيمة pKa له تساوي 5 . عندما تكون قيمة pH منخفضة يكون الحمض بالكامل تقريبا على شكل HA و عندما تكون قيمة pH مرتفعة تكون أيونات –A هي السائدة .
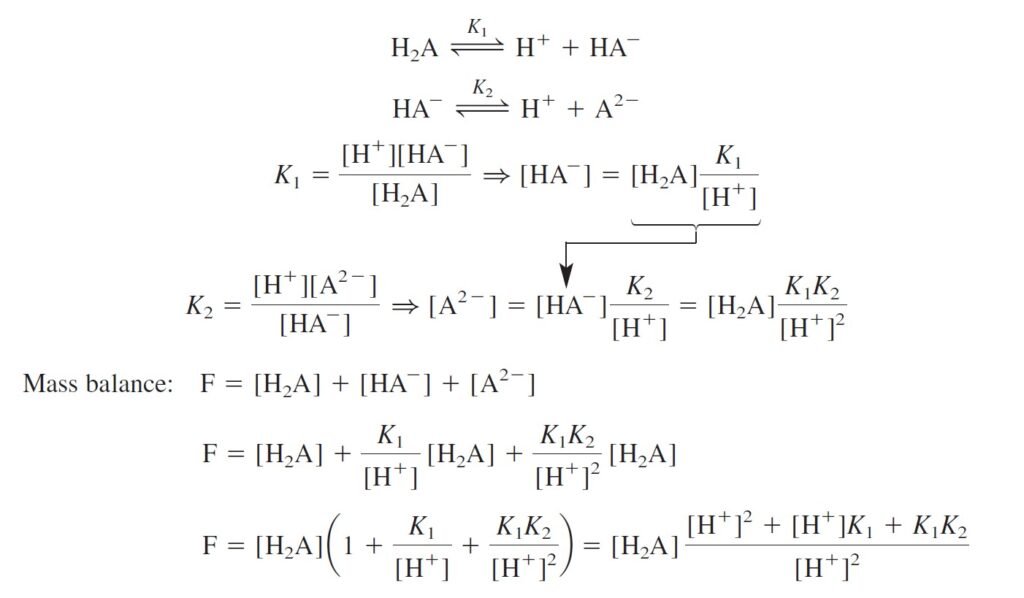
Diprotic System الأنظمة ثنائية البروتون
The derivation of fractional composition equations for a diprotic system follows the same pattern used for the monoprotic system.
إن الأسلوب المستخدم لاشتقاق معادلات التركيب الجزئي لنظام ثنائي البروتون يشابه النمط المستخدم في النظام أحادي البروتون.

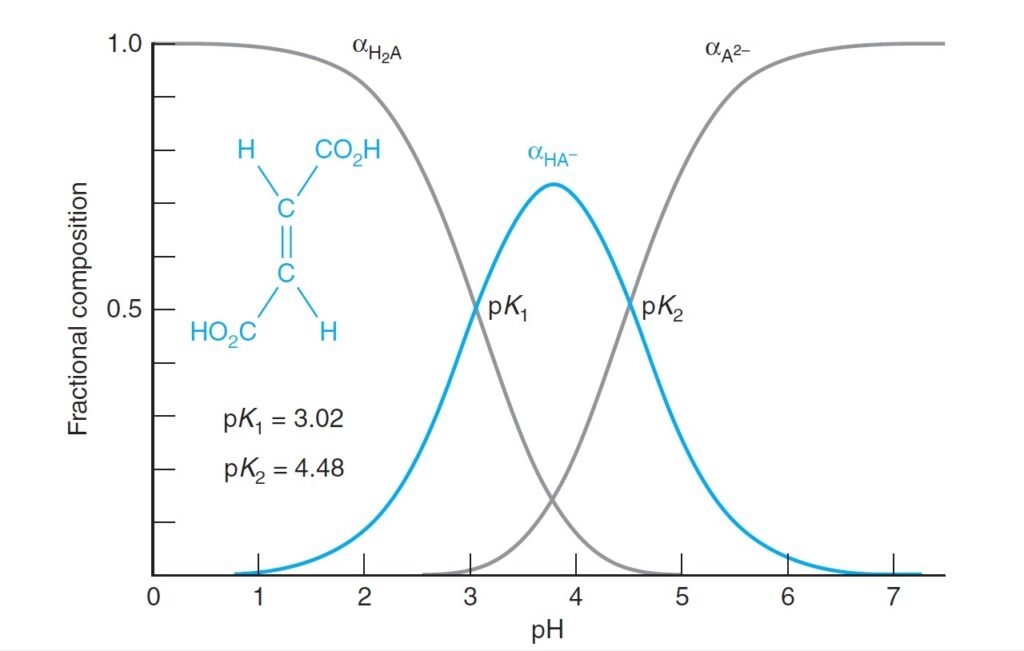
From below figure we noticed that at low pH, H2A is dominant. At intermediate pH, HA– is dominant; and, at high pH, A2– dominates.
من الشكل أدناه نلاحظ أن عندما تكون قيمة الرقم الهيدروجيني pH منخفضة فإن H2A تكون هي السائدة، و عندما تكون قيمة pH وسط تكون أيونات –HA هي السائدة، و عندما تكون قيم pH مرتفعة تكون أيونات –A2 هي السائدة .
المصادر:
- Quantitative Chemical Analysis by Daniel C. Harris, 8th Edition
- الموسوعة العلمية الكيميائية للأستاذ أكرم العلي
بوسترات (لوحات) كيميائية بدقة عالية (أكثر من 25 لوحة) من تصميم الأستاذ أكرم أمير العلي
تطبيقات كيميائية من تصميم الأستاذ أكرم امير العلي متوفر للجوالات التي تعمل بنظام أندرويد android على سوق جوجل بلاي google play
1 – تطبيق ملصقات الجدول الدوري باللغة العربية : بطاقات تحتوي على معلومات شاملة و مختصرة في نفس الوقت كل عنصر على حدة (اللغة العربية).
 مصادر الكيمياء موقع لتعليم الكيمياء بصورة مبسطة
مصادر الكيمياء موقع لتعليم الكيمياء بصورة مبسطة