الفعالية و المعالجة المنهجية للإتزان
Activity and the Systematic treatment of Equilibrium
( Sections 7.4 – 7.5, Quantitative Chemical Analysis by Daniel C. Harris, 8th Edition )
( التحليل الكيميائي النوعي – دانيال هاريس )
7 – 4 المعالجة المنهجية للإتزان
7 – 4 Systematic Treatment of Equilibrium
The systematic treatment of equilibrium is a way to deal with all types of chemical equilibria, regardless of their complexity.
المعالجة المنهجية للإتزان هي طريقة للتعامل مع جميع أنواع الإتزان الكيميائي بغض النظر عن مدى تعقيدها.
After setting up general equations, we often introduce specific conditions or judicious approximations that allow simplification.
بعد إعداد المعادلات العامة ، غالبًا ما نقدم شروطًا محددة أو تقديرات تقريبية حكيمة تسمح لنا بعملية التبسيط.
The systematic procedure is to write as many independent algebraic equations as there are unknowns (species) in the problem.
فالطريقة المنهجية تقوم على مبدأ كتابة معادلات رياضية منفصلة بعدد الدقائق (الجسيمات) المجهولة في المسألة .
The equations are generated by writing all the chemical equilibrium conditions plus two more: the balances of charge and of mass.
يتم كتابة المعادلات عن طريق كتابة جميع شروط الاتزان الكيميائي بالإضافة إلى “شرطين” آخرين: توازن الشحنة و توازن الكتلة.
There is only one charge balance in a given system, but there could be several mass balances.
قد يكون هناك توازن وحيد للشحنة في النظام و لكن قد يكون هناك أيضا توازنات عدبدة للكتل .
توازن الشحنة Charge Balance
The charge balance is an algebraic statement of electroneutrality: The sum of the positive charges in solution equals the sum of the negative charges in solution.
توازن الشحنة هي صيغة رياضية (حسابية) للإتزان الإلكتروني: أي : مجموع الشحنات الموجبة في المحلول يساوي مجموع الشحنات السالبة في المحلول.
Σ(+) charges = Σ(–) charges
Remember, the natural species not mentioned in the charge balance equation and The coefficient in front of each species always equals the magnitude of the charge on the ion.
تذكر هنا أن المركبات أو الجسيمات المتعادلة لا يتم ذكرها في معادلة توازن الشحنة و أيضا تذكر أن المعامل الموجود أمام كل جسيم يساوي دائمًا حجم الشحنة على ذلك الجسيم أو الأيون.
Example1 : Write the charge balance for a solution containing the following ionic species:
مثال1 : أكتب معادلة توازن الشحنة لمحلول يحتوي على الأيونات الآتية :
H2O, H+, OH–, K+, H2PO4– , HPO42–, and PO43–
Solution: Neutral specie (H2O) contribute no charge, so the charge balance is:
الحل : لاحظ هنا أن الماء H2O متعادل (و كذلك أي مركب متعادل آخر) لذلك لن يتم إدراجها في معادلة توازن الشحنة:
[H+] + [K+] = [OH–] + [H2PO4–] + 2[HPO42–] + 3[PO43–]
NOTE : total charge contributed by H+ and K+ equals the magnitude of the charge contributed by all of the anions on the right side of the equation. The coefficient in front of each species always equals the magnitude of the charge on the ion.
ملاحظة: إن إجمالي الشحنة التي ساهمت بها كل من +H و +K يساوي حجم جميع الشحنات التي ساهمت بها جميع الأنيونات (الأيونات السالبة) على الجانب الأيمن من المعادلة. كما لاحظ أيضا أن المعاملات (باللون الأحمر) قيمتها مساوية لمقدار قوة الشحنة و قد تم ذكرها في المعادلة لأن قيمتها أكبر من 1 .
فالأيون –PO43 و حسب معادلة توازن الشحنة يساهم بثلاثة مولات شحنتها سالبة، فلو كان تركيز أيون –PO43 يساوي 0.01 مول /لتر ، فإن قيمة الشحنة السالبة التي يساهم بها ذلك الأيون تساوي:
3[PO43–] = 3(0.01) = 0.03M
و لكن، هل معادلة توازن الشحنة المذكورة اعلاه موزونة رغم أن عدد الشحنات السالبة في الطرف الأيمن من المعادلة أكثر من عدد الشحنات الموجبة في الطرف الأيمن؟ الإجابة “نعم” المعادلة موزونة رغم ذلك الاختلاف في العدد. فلو فرضنا أننا نريد أن حضر محلولا حجمه لترا واحدا من خلط محلولين مع بعضهما البعض و هما : محلول KH2PO4 تركيزه 0.025 مول/لتر و محلول KOH تركيزه 0.030 مول/لتر ، و عند الاتزان تم حساب تراكيز جميع الجسيمات (الدقائق) الموجودة في المحلول و كانت القراءات كالآتي:
[H+] = 5.1 × 10−12 M [H2PO4–] = 1.3 × 10−6 M
[K+] = 0.055 M [HPO42–] = 0.022 M
[OH–] = 0.002 M [PO43–] = 0.003 M
و عند حساب التراكيز رياضيا نجد أن:
[H+] + [K+] = [OH–] + [H2PO4–] + 2[HPO42–] + 3[PO43–]
5.1 × 10−12 + 0.055 = 0.002 + 1.3 × 10−6 + 2(0.022) + 3(0.003)
0.055 M = 0.055 M
و نلاحظ هنا أن مجموع الشحنة الموجبة يساوي 0.055 مول/لتر و هو يساوي مجموع الشحنة السالبة و الذي يساوي أيضا 0.055 مول/لتر ، و هو ما يزهرة الشكل أدناه .
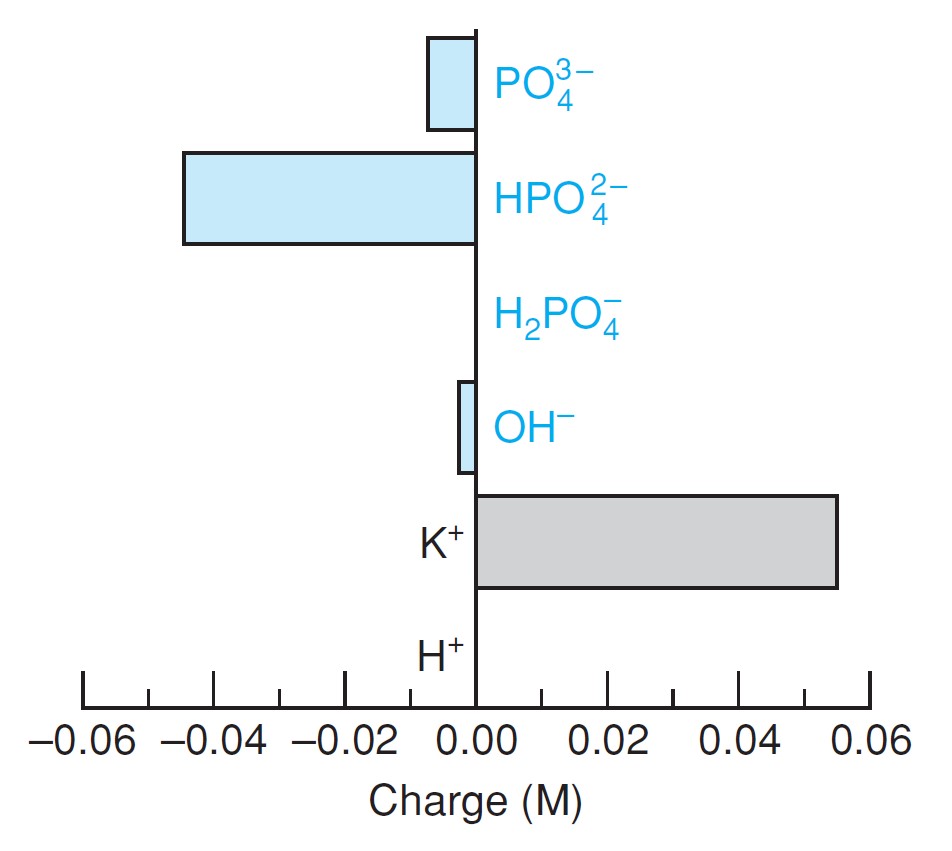
The general form of the charge balance for any solution is
عموما، الشكل العام لمعادلة توازن الشحنة لأي محلول هو :
n1[C1] + n2[C2] + … = m1[A1] + m2[A2] + …
where [C] is the concentration of a cation, n is the charge of the cation, [A] is the concentration of an anion, and m is the magnitude of the charge of the anion.
حيث [C] تركيز الكاتيون و n شحنة الكاتيون و [A] تركيز الأنيون و m هو شحنة الأنيون.
Example2 : Write the charge balance for a solution containing the following ionic species:
مثال2 : أكتب معادلة توازن الشحنة لمحلول يحتوي على الأيونات الآتية :
H2O, H+, OH–, K+, ClO4– , Fe(CN)63–, CN– , Fe3+ , Mg2+ , CH3OH , HCN , NH3 and NH4+
Solution: Neutral species (H2O, CH3OH, HCN, and NH3) contribute no charge, so the charge balance is:
الحل : لاحظ هنا أن H2O و CH3OH و HCN و NH3 جميعها متعادلة لذلك لن يتم إدراجها في معادلة توازن الشحنة:
[H+] + 3[Fe3+] + 2[Mg2+] + [NH4+] = [OH–] + [ClO4–] + 3[Fe(CN)63–] + [CN–]
توازن الكتلة Mass Balance
The mass balance, also called the material balance, is a statement of the conservation of matter. The mass balance states that the quantity of all species in a solution containing a particular atom (or group of atoms) must equal the amount of that atom (or group) delivered to the solution.
توازن الكتلة يعرف أيضا باسم توازن المواد، و هي تعبير عن حفظ المادة. و ينص قانون توازن الكتلة على أن كمية جميع الدقائق أو الجسيمات الموجودة في محلول الذي يحتوي على ذرة معينة (أو مجموعة ذرات) يجب أن تساوي كمية تلك الذرة (أو مجموعة الذرات) التي يتم إداخلها إلى المحلول.
Suppose that a solution is prepared by dissolving 0.050 mol of acetic acid in water to give a total volume of 1.00 L. Acetic acid partially dissociates into acetate:
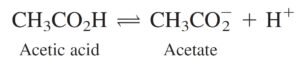
لنفترض أن لدينا محلولا تم تحضيره بتذويب محلول لحمض الخليك تركيزه 0.050 مول/لتر و أضفنا إليه الماء المقطر حتى حصلنا على محلول نهائي حجمه لترا واحدا. في هذا المحلول سنلاحظ أن حمض الخليك قد تفكك جزئيا إلى أيون الخلات، أي أنه أصبح لدينا في ذات المحلول أيونات الخلات التي نتجت من تفكك حمض الخليك بالإضافة إلى بقايا لحمض الخليك التي لم تتفكك بالأصل :

The mass balance states that the quantity of dissociated and undissociated acetic acid in the solution must equal the amount of acetic acid put into the solution.

و ينص قانون توازن الكتلة على أن كمية أيونات الخلات بالإضافة إلى كمية حمض الخليك التي لم تتفكك تساوي كمية حمض الخليك التي تم إدخالها إلى المحلول بالأصل.

Also, suppose that a solution is prepared by dissolving 0.0250 mol of Phosphoric acid in water to give a total volume of 1.00 L. Phosphoric acid dissociates to H2PO4– , HPO42– and PO43– ions, the mass balance for the solution is:
و لنفترض أيضا أن لدينا محلولا تم تحضيره بتذويب محلول لحمض الفوسفوريك تركيزه 0.0250 مول/لتر و أضفنا إليه الماء المقطر حتى حصلنا على محلول نهائي حجمه لترا واحدا. في هذا المحلول سنلاحظ أن حمض الفوسفوريك قد تفكك جزئيا إلى أيونات –H2PO4 و –HPO42 و –PO43 ، لذلك فإن معادلة توازن الكتلة للمحلول هي:
0.025 M = [H3PO4] + [H2PO4–] + [HPO42–] + [PO43–]
Example3 : Write the mass balances for K+ and for phosphate in a solution prepared by mixing 0.025 mol KH2PO4 plus 0.030 mol KOH and diluting to 1.00 L.
مثال3 : أكتب معادلة توازن الكتلة لأيونات البوتاسيوم +K و الفوسفات في محلول تم تحضيره عن طريق خلط محلول KH2PO4 تركيزه 0.025 مول/لتر مع محلول KOH تركيزه 0.030 و تم تخفيف الخليط السابق بالماء المقطر حتى خصلنا على محلول حجمه 1 لتر .
Solution: The total K+ is 0.025 M + 0.030 M, so one mass balance is:
الحل : تركيز أيون البوتاسيوم +K الكلي يساوي 0.025 مول/لتر + 0.030 مول/لتر ،لذلك فإن تركيز أيون البوتاسيوم يساوي :
[K+] = 0.055 0 M
The total of all forms of phosphate is 0.025 M, so the mass balance for phosphate is:
كما أن مجمل جميع أشكال أيونات الفوسفات تساوي 0.025 مول/لتر، و بالتالي فإن معادلة توازن الكتلة للفوسفات تساوي :
[H3PO4] + [H2PO4–] + [HPO42–] + [PO43–] = 0.025 M
المعالجة المنهجية للإتزان
Systematic Treatment of Equilibrium
- Step 1 Write the pertinent reactions.
- Step 2 Write the charge balance equation
- Step 3 Write mass balance equations. There may be more than one.
- Step 4 Write the equilibrium constant expression for each chemical reaction. This step is the only one in which activity coefficients appear.
- Step 5 Count the equations and unknowns. There should be as many equations as unknowns (chemical species). If not, you must either find more equilibria or fix some concentrations at known values.
- Step 6 Solve for all unknowns.
الخطوة 1 كتابة التفاعلات ذات الصلة.
الخطوة 2 كتابة معادلة توازن الشحنة.
الخطوة 3 كتابة معادلات توازن الكتلة. قد يكون هناك أكثر من واحدة.
الخطوة 4 كتابة معادلة الثابت الاتزان لكل تفاعل كيميائي. هذه الخطوة هي الوحيدة التي تظهر فيها معاملات الفعالية أو معاملات النشاط.
الخطوة 5 حساب و عد المعادلات و المجاهيل. يجب أن يكون هناك العديد من المعادلات مساوية لعدد المجاهيل (الجسيمات و الدقائق الكيميائية). إذا لم يكن الأمر كذلك ، فيجب عليك إما العثور على مزيد من التوازنات أو إصلاح بعض التركيزات بقيم معروفة.
الخطوة 6 حل كل المجاهيل.
7 – 5 تطبيق المعالجة المنهجية للإتزان
7 – 5 Applying the Systematic Treatment of Equilibrium
A Solution of Ammonia
Let’s find the concentrations of species in an aqueous solution containing 0.010 0 mol NH3 in 1.000 L.
محلول الأمونيا
لنحسب تراكيز الجسيمات أو الدقائق الموجودة في محلول مائي حجمه 1 لتر يحتوي على الأمونيا NH3 بتركيز 0.010 مول/لتر .
The primary and secondary equilibriums is:
![]() ………..( 1 )
………..( 1 )
![]() ………..( 2 )
………..( 2 )
In this problem our goal is to find .
في هذه المسأله هدفنا إيجاد تراكيز كل من
[NH3], [NH4+], [H+], and [OH–]
Step 1 Pertinent reactions. They are as shown above
الخطوة 1 كتابة التفاعلات ذات الصلة، تم القيام بهذه الخطوة مسبقا و كما هو يظهر اعلاه.
Step 2 Charge balance. The sum of positive charge equals the sum of negative charge:
الخطوة 2 كتابة معادلة توازن الشحنة. يجب أن قيمة الشحنات في كلا الطرفين متساوية ، لاحظ أن لدنا NH3 و +NH4 و +H و –OH ، و حيث أن NH3 لا شحنة لها فسوف نتجاهلها
![]() ………..( 3 )
………..( 3 )
Step 3 Mass balance. All of the ammonia delivered to the solution is either in the form NH3 or NH4+ .
الخطوة 3 كتابة معادلات توازن الكتلة. جميع الأمونيا الموجود في المحلول تكون على شكل NH3 غير متفكك أو على شكل أيون +NH4 .
![]()
………..( 4 )
حيث F تمثل التركيز الأساسي .
Step 4 Equilibrium expressions.
الخطوة 4 كتابة معادلة الثابت الاتزان لكل تفاعل كيميائي.
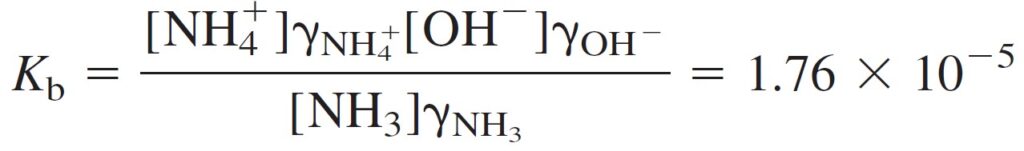
………..( 5 )
![]()
………..( 6 )
Step 5 Count equations and unknowns. We have four equations, 3 to 6, and four unknowns ([NH3], [NH4+], [H+], and [OH–]).
الخطوة 5 حساب و عد المعادلات و المجاهيل. في هذه المسألة لدينا اربعة معادلات من 3 الى 6 و لدينا ايضا أربعة مجاهيل ([NH3] و [+NH4] و [+H] و [–OH])
Step 6 Solve.
الخطوة 6 حل كل المجاهيل
We have four equations with four unknowns, so it is algebraically possible to solve.
لدينا أربعة مجاهيل، لذلك من الناحية الرياضية (الحسابية) يمكن حلها.
first, we start by assuming all activity coefficients are 1, then choose one species to solve for. e.g. [H+] is a good choice for acid-base problems.
أولاً ، نبدأ بافتراض أن جميع معاملات الفعالية تساوي 1 ، ثم نحتار جسيم واحدًا لحلها. على سبيل المثال [+H] اختيار جيد لمسائل الحمض-القاعدة.
Then we arrange all our equations and make substitutions so that we end up with one equation with one unknown.
ثم نرتب كل معادلاتنا ونجري عمليات استبدال حتى ننتهي بمعادلة واحدة بها مجهول واحد.
Which of four equations do we want to target for substitutions? We will make rearrangements of three equations and then plug them into the fourth.
فأي من المعادلات الأربع (3 إلى 6) نريد أن نعتمدها لإجراء الاستبدالات فيها؟ و هنا سنعيد ترتيب المعادلات الثلاث الاخرى ثم نعوض بها في المعادلة الرابعة.
We recommend targeting the equation that contains the most unknows variables, i.e. we will choose equation number 5.
نوصي باستهداف المعادلة التي تحتوي على أكثر المتغيرات المجهولة ، أي أننا نوصي باختيار المعادلة رقم 5.
Since [OH–] = Kw/[H+], putting this expression for [OH–] in equation 3 we get:
حيث أن OH–] = Kw/[H+]] ، و بالتعويض بهذا التعبير في المعادلة رقم 3 ، سنحصل على :

from which we can solve for [NH4+]:
و بإعادة ترتيب العلاقة السابقة يمكن حساب [+NH4] :
 ………..( 7 )
………..( 7 )
By substituting the expression for [NH4+] from Equation 7 into the equation no. 4 we get:
عند استبدال قيمة [+NH4] التي حصلنا عليها من المعادلة 7 في المعادلة 4 نحصل على المعادلة الآتية :
 ………..( 8 )
………..( 8 )
by substituting our expressions for [NH4+], [NH3], and [OH–] into the Kb equilibrium (equation no.5) we get:
و من خلال استبدال القيم الخاصة ب [+NH4] و [NH3] و [–OH] في المعادلة رقم 5 نحصل على المعادلة الآتية :
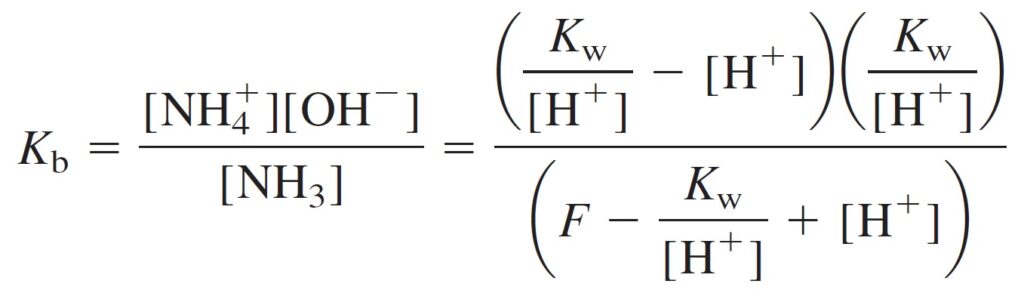 ………..( 9 )
………..( 9 )
In equation no. 9 we knowns the values of Kb, Kw and F, but [H+] is the only unknown.
في المعادلة رقم 9 معلوم لدينا قيم Kb و Kw و F ، لكن قيمة [+H] هو المجهول الوحيد.
One way you could solve for [H+] is to guess a value of [H+], put it into the right side of the equation, and see if the right side is equal to Kb on the left side. So guess a little smaller value of [H+] and see if you come closer to Kb. Continue guessing smaller values of [H+] until you have solved the equation. Or you can guess larger values of [H+] until you have solved the equation.
إحدى الطرق التي يمكنك حل هذه المسألة هي تخمين قيمة [+H] ووضعها في الجانب الأيمن من المعادلة ومعرفة ما إذا كان الجانب الأيمن يساوي Kb على الجانب الأيسر. لذلك خمن قيمة صغيرة قليلاً لـ [+H] ومعرفة ما إذا كنت تقترب من Kb. و استمر في تخمين القيم الأصغر لـ [+H] حتى تحل المعادلة. كما باستطتعتك تخمين قيمًا أكبر لـ [+H] حتى تحل المعادلة.
After solving for [H+], we could calculate[OH–] = Kw/[H+]. We could find [NH4+] from Equation 7 and we could compute [NH3] from equation 9.
بعد حل [+H] ، يمكننا حساب OH–] = Kw/[H+]]. كما يمكننا إيجاد [+NH4] من المعادلة 7 ويمكننا حساب [NH3] المعادلة رقم 9.
المصادر:
- كتاب Quantitative Chemical Analysis by Daniel C. Harris
- الموسوعة العلمية الكيميائية للأستاذ أكرم العلي
بوسترات (لوحات) كيميائية بدقة عالية (أكثر من 25 لوحة) من تصميم الأستاذ أكرم أمير العلي
تطبيقات كيميائية من تصميم الأستاذ أكرم امير العلي متوفر للجوالات التي تعمل بنظام أندرويد android على سوق جوجل بلاي google play
1 – تطبيق ملصقات الجدول الدوري باللغة العربية : بطاقات تحتوي على معلومات شاملة و مختصرة في نفس الوقت كل عنصر على حدة (اللغة العربية).
https://play.google.com/store/apps/details?id=com.akramir2
 مصادر الكيمياء موقع لتعليم الكيمياء بصورة مبسطة
مصادر الكيمياء موقع لتعليم الكيمياء بصورة مبسطة